
设M是△ABC内一点,且△ABC的面积为1,定义f(M)=(m,n,p),其中m、n、p分别是△MBC,△MCA,△MAB的面积,若f(M)=( ,x,y),则
,x,y),则 +
+ 的最小值是( )
的最小值是( )
A.8 B.9 C.16 D.18
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:高中数学 来源:[同步]2014年湘教版必修三 7.1 解析几何初步练习卷(解析版) 题型:填空题
(5分)从点(2,3)射出的光线沿与直线x﹣2y=0平行的直线射到y轴上,则经y轴反射的光线所在的直线方程为 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教B版选修4-5 2.3平均值不等式练习卷(解析版) 题型:选择题
若a,b,c∈R+,且a+b+c=6,则lga+lgb+lgc的取值范围是( )
A.(﹣∞,lg6] B.(﹣∞,3lg2] C.[lg6,+∞) D.[3lg2,+∞)
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教B版选修4-5 2.3平均值不等式练习卷(解析版) 题型:选择题
已知x,y,z∈R,且x+y+z=8,x2+y2+z2=24,则x的取值范围是( )
A.[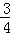 ,4] B.[
,4] B.[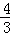 ,4] C.[
,4] C.[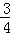 ,3] D.[
,3] D.[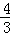 ,3]
,3]
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教B版选修4-5 2.2排序不等式练习卷(解析版) 题型:选择题
若a<b<c,x<y<z,则下列各式中值最大的一个是( )
A.ax+cy+bz B.bx+ay+cz C.bx+cy+az D.ax+by+cz
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教B版选修4-5 1.4绝对值的三角不等式练习卷(解析版) 题型:选择题
若关于x的不等式|x+1|﹣|x﹣2|<a2﹣4a有实数解,则实数a的取值范围为( )
A.(﹣∞,1)∪(3,+∞) B.(1,3)
C.(﹣∞,﹣3)∪(﹣1,+∞) D.(﹣3,﹣1)
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教B版选修4-5 1.2基本不等式练习卷(解析版) 题型:选择题
(2014•潍坊模拟)若a>0,b>0,且a+b=4,则下列不等式中恒成立的是( )
A.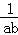 >
>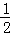 B.
B. +
+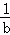 ≤1 C.
≤1 C.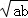 ≥2 D.
≥2 D. ≤
≤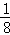
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com