
【题目】已知一个正四面体和一个正四棱锥,它们的各条棱长均相等,则下列说法:
①它们的高相等;②它们的内切球半径相等;③它们的侧棱与底面所成的线面角的大小相等;④若正四面体的体积为![]() ,正四棱锥的体积为
,正四棱锥的体积为![]() ,则
,则![]() ;⑤它们能拼成一个斜三棱柱.其中正确的个数为( )
;⑤它们能拼成一个斜三棱柱.其中正确的个数为( )
A.1个B.2个C.3个D.4个
【答案】B
【解析】
①,正四面体的高![]() ,正四棱锥的高
,正四棱锥的高![]() ,所以该命题错误;
,所以该命题错误;
②,设正四面体的内切球半径为![]()
![]() .设正四棱锥的内切球半径为
.设正四棱锥的内切球半径为![]() 则
则![]() .所以该命题不正确;
.所以该命题不正确;
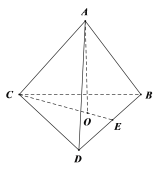
③,在正四面体中,![]() 就是侧棱和底面所成的角,
就是侧棱和底面所成的角,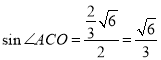 .在正四棱锥中,
.在正四棱锥中,![]() 就是侧棱和底面所成的角,
就是侧棱和底面所成的角,![]() ,所以该命题不正确;
,所以该命题不正确;
④,计算得![]() .所以该命题正确;
.所以该命题正确;
⑤,把一个斜三棱柱分解成一个正四面体和正四棱锥,所以该命题正确.
设正四面体和正四棱锥的棱长都为![]() ,
,
①,![]() ,
,
所以正四面体的高![]() .
.
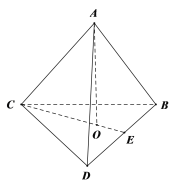
如图,正四棱锥的棱长都为2,它的高![]() ,
,
所以该命题不正确;
②,设正四面体的内切球半径为![]()
则![]() ,所以
,所以![]() .
.
设正四棱锥的内切球半径为![]() 则
则
![]() ,所以
,所以![]() .
.
所以该命题不正确;
③,在正四面体中,![]() 就是侧棱和底面所成的角,
就是侧棱和底面所成的角,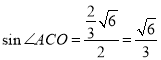 .
.
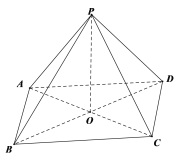
在正四棱锥中,![]() 就是侧棱和底面所成的角,
就是侧棱和底面所成的角,![]() ,
,
所以该命题不正确;
④,若正四面体的体积为![]() ,
,![]() ,
,
正四棱锥的体积为![]() ,
,![]() ,则
,则![]() .
.
所以该命题正确;
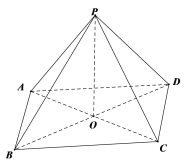
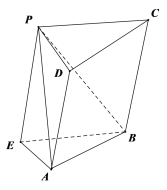
⑤,如图,是一个斜三棱柱,其中四棱锥![]() 是一个棱长都为2的正四棱锥,四面体
是一个棱长都为2的正四棱锥,四面体![]() 是棱长都为2的正四面体,所以它们能拼成一个斜三棱柱.所以该命题正确.
是棱长都为2的正四面体,所以它们能拼成一个斜三棱柱.所以该命题正确.
故选:B.


科目:高中数学 来源: 题型:
【题目】某学校近几年来通过“书香校园”主题系列活动,倡导学生整本阅读纸质课外书籍.下面的统计图是该校2013年至2018年纸质书人均阅读量的情况,根据统计图提供的信息,下列推断不合理的是( )
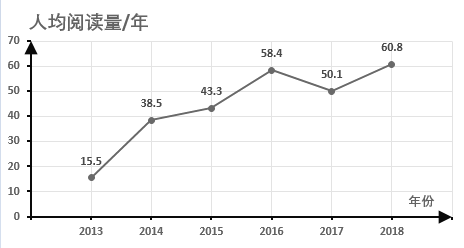
A.从2013年到2016年,该校纸质书人均阅读量逐年增长
B.2013年至2018年,该校纸质书人均阅读量的中位数是46.7本
C.2013年至2018年,该校纸质书人均阅读量的极差是45.3本
D.2013年至2018年,该校后三年纸质书人均阅读量总和是前三年纸质书人均阅读量总和的2倍
查看答案和解析>>
科目:高中数学 来源: 题型:
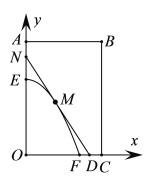
【题目】如图,某小区有一块矩形地块![]() ,其中
,其中![]() ,
,![]() ,单位:百米.已知
,单位:百米.已知![]() 是一个游泳池,计划在地块
是一个游泳池,计划在地块![]() 内修一条与池边
内修一条与池边![]() 相切于点
相切于点![]() 的直路
的直路![]() (宽度不计),交线段
(宽度不计),交线段![]() 于点
于点![]() ,交线段
,交线段![]() 于点
于点![]() .现以点
.现以点![]() 为坐标原点,以线段
为坐标原点,以线段![]() 所在直线为
所在直线为![]() 轴,建立平面直角坐标系,若池边
轴,建立平面直角坐标系,若池边![]() 满足函数
满足函数![]() 的图象,若点
的图象,若点![]() 到
到![]() 轴距离记为
轴距离记为![]() .
.
(1)当![]() 时,求直路所在的直线方程;
时,求直路所在的直线方程;
(2)当![]() 为何值时,地块
为何值时,地块![]() 在直路
在直路![]() 不含泳池那侧的面积取到最大,最大值时多少?
不含泳池那侧的面积取到最大,最大值时多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从甲、乙两种树苗中各抽测了10株树苗的高度,其茎叶图数据如图.根据茎叶图,下列描述正确的是( )
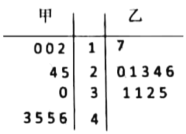
A.甲种树苗的中位数大于乙种树苗的中位数,且甲种树苗比乙种树苗长得整齐
B.甲种树苗的中位数大于乙种树苗的中位数,但乙种树苗比甲种树苗长得整齐
C.乙种树苗的中位数大于甲种树苗的中位数,且乙种树苗比甲种树苗长得整齐
D.乙种树苗的中位数大于甲种树苗的中位数,但甲种树苗比乙种树苗长得整齐
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)求![]() 在点P(1,
在点P(1,![]() )处的切线方程;
)处的切线方程;
(2)若关于x的不等式![]() 有且仅有三个整数解,求实数t的取值范围;
有且仅有三个整数解,求实数t的取值范围;
(3)若![]() 存在两个正实数
存在两个正实数![]() ,
,![]() 满足
满足![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为等差数列,
为等差数列,![]() ,
,![]() ,
,![]() 分别是下表第一、二、三行中的某一个数,且
分别是下表第一、二、三行中的某一个数,且![]() ,
,![]() ,
,![]() 中的任何两个数都不在下表的同一列.
中的任何两个数都不在下表的同一列.
第一列 | 第二列 | 第三列 | |
第一行 | |||
第二行 | 4 | 6 | 9 |
第三行 | 12 | 8 | 7 |
请从①![]() ,②
,②![]() ,③
,③ ![]() 的三个条件中选一个填入上表,使满足以上条件的数列
的三个条件中选一个填入上表,使满足以上条件的数列![]() 存在;并在此存在的数列
存在;并在此存在的数列![]() 中,试解答下列两个问题
中,试解答下列两个问题
(1)求数列![]() 的通项公式;
的通项公式;
(2)设数列![]() 满足
满足![]() ,求数列
,求数列![]() 的前n项和
的前n项和![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com