
【题目】某地棚户区改造建筑平面示意图如图所示,经规划调研确定,棚改规划建筑用地区域近似为圆面,该圆面的内接四边形![]() 是原棚户区建筑用地,测量可知边界
是原棚户区建筑用地,测量可知边界![]() 万米,
万米,![]() 万米,
万米,![]() 万米.
万米.
(1)请计算原棚户区建筑用地![]() 的面积及
的面积及![]() 的长;
的长;
(2)因地理条件的限制,边界![]() 不能更改,而边界
不能更改,而边界![]() 可以调整,为了提高棚户区建筑用地的利用率,请在圆弧
可以调整,为了提高棚户区建筑用地的利用率,请在圆弧![]() 上设计一点
上设计一点![]() ,使得棚户区改造后的新建筑用地
,使得棚户区改造后的新建筑用地![]() 的面积最大,并求出最大值.
的面积最大,并求出最大值.

【答案】(1) ![]() 万米.
万米. ![]() 万平方米.
万平方米.
(2) 所求面积的最大值为![]() 万平方米,此时点
万平方米,此时点![]() 为弧ABC的中点.
为弧ABC的中点.
【解析】试题分析:(1)利用圆内接四边形得到对角互补,再利用余弦定理求出相关边长,再利用三角形的面积公式和分割法进行求解 ;(2)利用余弦定理和基本不等式进行求解.
试题解析:(1)根据题意知,四边形ABCD内接于圆,∴∠ABC+∠ADC=180°.
在△ABC中,由余弦定理,得AC2=AB2+BC2-2AB·BC·cos∠ABC,
即AC2=42+62-2×4×6×cos∠ABC.
在△ADC中,由余弦定理,得
AC2=AD2+DC2-2AD·DC·cos∠ADC,即AC2=42+22-2×4×2×cos∠ADC.
又cos∠ABC=-cos∠ADC,
∴cos∠ABC=![]() ,AC2=28,即AC=2
,AC2=28,即AC=2![]() 万米,
万米,
又∠ABC∈(0,π),∴∠ABC=![]() .
.
∴S四边形ABCD=S△ABC+S△ADC=![]() ×4×6×sin
×4×6×sin![]() +
+![]() ×2×4×sin
×2×4×sin![]() =8
=8![]() (平方万米).
(平方万米).
(2)由题意知,S四边形APCD=S△ADC+S△APC,
且S△ADC=![]() AD·CD·sin
AD·CD·sin![]() =2
=2![]() (平方万米).
(平方万米).
设AP=x,CP=y,则S△APC=![]() xysin
xysin![]() =
=![]() xy.
xy.
在△APC中,由余弦定理,得AC2=x2+y2-2xy·cos![]() =x2+y2-xy=28,
=x2+y2-xy=28,
又x2+y2-xy≥2xy-xy=xy,
当且仅当x=y时取等号,∴xy≤28.
∴S四边形APCD=2![]() +
+![]() xy≤2
xy≤2![]() +
+![]() ×28=9
×28=9![]() (平方万米),
(平方万米),
故所求面积的最大值为9![]() 平方万米,此时点P为
平方万米,此时点P为![]() 的中点.
的中点.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆的一个顶点为A(0,-1),焦点在x轴上。若右焦点F到直线x-y+2![]() =0的距离为3。
=0的距离为3。
(1)求椭圆的方程;
(2)设直线y=kx+m(k≠0)与椭圆相交于不同的两点M、N。当|AM|=|AN|时,求m的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 是平面,
是平面,![]() ,
,![]() 是直线,给出下列命题:
是直线,给出下列命题:
①若![]() ,
,![]() ,则
,则![]() ;
;
②若![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ;
;
③如果![]() ,
,![]() ,
,![]() ,
,![]() 是异面直线,则
是异面直线,则![]() 与
与![]() 相交;
相交;
④若![]() .
.![]() ,且
,且![]() ,
,![]() ,则
,则![]() ,且
,且![]()
其中正确确命题的序号是_____(把正确命题的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,上顶点
,上顶点![]() 到直线
到直线![]() 的距离为
的距离为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)是否存在过点![]() 的直线
的直线![]() 与椭圆交于不同的两点
与椭圆交于不同的两点![]() ,线段
,线段![]() 的中点为
的中点为![]() ,使得
,使得![]() ?若存在,求直线
?若存在,求直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2015 年 12 月,华中地区数城市空气污染指数“爆表”,此轮污染为 2015 年以来最严重的污染过程,为了探究车流量与![]() 的浓度是否相关,现采集到华中某城市 2015 年 12 月份某星期星期一到星期日某一时间段车流量与
的浓度是否相关,现采集到华中某城市 2015 年 12 月份某星期星期一到星期日某一时间段车流量与![]() 的数据如表:
的数据如表:
时间 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 |
车流量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 28 | 30 | 35 | 41 | 49 | 56 | 62 |
(1)由散点图知![]() 与
与![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程;(提示数据:
的线性回归方程;(提示数据: ![]() )
)
(2)利用(1)所求的回归方程,预测该市车流量为 12 万辆时![]() 的浓度.
的浓度.
参考公式:回归直线的方程是![]() ,
,
其中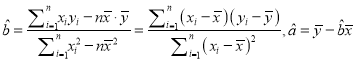 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
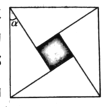
【题目】中国古代的数学家们最早发现并应用勾股定理,而最先对勾股定理进行证明的是三国时期的数学家赵爽.赵爽创制了一幅“勾股圆方图”,用数形结合的方法,给出了勾股定理的详细证明。在这幅“勾股圆方图”中,![]() 个相等的直角三角形再加上中间的那个小正方形组成一个大的正方形。若直角三角形的较小锐角
个相等的直角三角形再加上中间的那个小正方形组成一个大的正方形。若直角三角形的较小锐角![]() 的正切值为
的正切值为![]() ,现向该正方形区域内投掷-枚飞镖,则飞镖落在小正方形内(阴影部分)的概率是( )
,现向该正方形区域内投掷-枚飞镖,则飞镖落在小正方形内(阴影部分)的概率是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】容器中盛有5个白乒乓球和3个黄乒乓球.
(1)“从8个球中任意取出1个,取出的是白球”与“从剩下的7个球中任意取出1个,取出的还是白球”这两个事件是否相互独立?为什么?
(2)“从8个球中任意取出1个,取出的是白球”与“把取出的1个白球放回容器,再从容器中任意取出1个,取出的是黄球”这两个事件是否相互独立?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com