
 已知正方体AC1的棱长为a,过B1作B1E⊥BD1于点E,过点E作EF⊥BD于F.
已知正方体AC1的棱长为a,过B1作B1E⊥BD1于点E,过点E作EF⊥BD于F.分析 (1)在平面BDD1中,EF⊥BD,D1D⊥BD,故EF∥D1D,由D1D∥A1A得FE∥A1A,故EF∥平面ABB1A1;
(2)由△BEB1∽△BB1D1可求得BE,再利用△BEF∽△BD1D求出FB,EF,在△ABF中由余弦定理解出AF,最后根据勾股定理计算AE.
解答  (1)证明:∵D1D⊥平面ABCD,BD?平面ABCD,
(1)证明:∵D1D⊥平面ABCD,BD?平面ABCD,
∴D1D⊥BD,∵EF⊥BD,EF?平面BD1D,D1D?平面BD1D,
∴EF∥D1D.∵D1D∥A1A,
∴EF∥A1A,又∵A1A?平面ABB1A1,EF?ABB1A1,
∴EF∥平面ABB1A1.
(2)∵正方体AC1的棱长为a,∴B1B=a,BD=$\sqrt{2}a$,BD1=$\sqrt{3}a$.
∵B1E⊥BD1,∴$\frac{{B}_{1}B}{B{D}_{1}}=\frac{BE}{{B}_{1}B}$,∴BE=$\frac{{B}_{1}{B}^{2}}{B{D}_{1}}$=$\frac{\sqrt{3}a}{3}$.
∵EF∥D1D,∴$\frac{EF}{{D}_{1}D}=\frac{BF}{BD}=\frac{BE}{B{D}_{1}}$=$\frac{1}{3}$,∴EF=$\frac{a}{3}$,BF=$\frac{\sqrt{2}a}{3}$.
连结AF,AE,在△ABF中,AB=a,∠ABF=45°,
∴AF=$\sqrt{{a}^{2}+(\frac{\sqrt{2}a}{3})^{2}-2a•\frac{\sqrt{2}a}{3}•\frac{\sqrt{2}}{2}}$=$\frac{\sqrt{5}a}{3}$.
∴AE=$\sqrt{A{F}^{2}+E{F}^{2}}$=$\sqrt{\frac{5{a}^{2}}{9}+\frac{{a}^{2}}{9}}$=$\frac{\sqrt{6}a}{3}$.
点评 本题考查了线面平行的判定,空间距离的计算,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
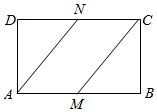 如图在长方形ABCD中,$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{AD}=\overrightarrow b,N$是CD的中点,M是线段AB上的点,$|{\overrightarrow a}|=2,|{\overrightarrow b}|=1$.
如图在长方形ABCD中,$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{AD}=\overrightarrow b,N$是CD的中点,M是线段AB上的点,$|{\overrightarrow a}|=2,|{\overrightarrow b}|=1$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,四边形ABCD与ABEF均为矩形,BC=BE=2AB,二面角E-AB-C的大小为$\frac{π}{3}$.现将△ACD绕着AC旋转一周,则在旋转过程中,( )
如图,四边形ABCD与ABEF均为矩形,BC=BE=2AB,二面角E-AB-C的大小为$\frac{π}{3}$.现将△ACD绕着AC旋转一周,则在旋转过程中,( )| A. | 不存在某个位置,使得直线AD与BE所成的角为$\frac{π}{4}$ | |
| B. | 存在某个位置,使得直线AD与BE所成的角为$\frac{π}{2}$ | |
| C. | 不存在某个位置,使得直线AD与平面ABEF所成的角为$\frac{π}{4}$ | |
| D. | 存在某个位置,使得直线AD与平面ABEF所成的角为$\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com