
已知函数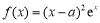 ,
,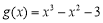 ,其中
,其中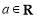 .
.
(1)当 时,求曲线
时,求曲线 在点
在点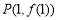 处的切线方程;
处的切线方程;
(2)若存在 ,使得
,使得 成立,求实数M的最大值;
成立,求实数M的最大值;
(3)若对任意的 ,都有
,都有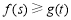 ,求实数
,求实数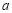 的取值范围.
的取值范围.
(1)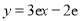 ;(2)
;(2)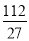 ;(3)
;(3)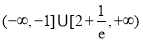 。
。
【解析】
试题分析:(1)根据导数的几何意义求出切线的斜率,然后利用点斜式求出切线的方程;(2)由题意知要使不等式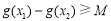 成立,需要
成立,需要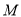 比左边的最小值即可,要求
比左边的最小值即可,要求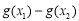 的最小值,只需求
的最小值,只需求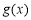 在
在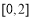 上的最小值与最大值然后作差。(3)由题意知,应求
上的最小值与最大值然后作差。(3)由题意知,应求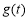 的最大值,
的最大值,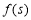 的最小值,在求
的最小值,在求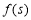 的最小值时,令
的最小值时,令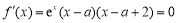 得
得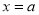 ,或
,或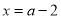 ,根据
,根据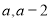 与区间
与区间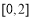 的关系分情况讨论。
的关系分情况讨论。
试题解析:(1)当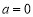 时,
时, 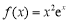 ,
,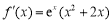 ,
,
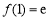 ,
,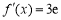 ,
,
所以所求切线方程为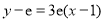 ,即
,即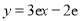 . 2分
. 2分
(2)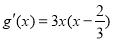 ,
,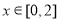 .令
.令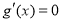 ,得
,得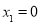 ,
,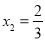 .
.
当x变化时,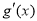 与
与 的变化情况如下:
的变化情况如下:
x | 0 |
|
|
| 2 |
|
| - | 0 | + |
|
|
|
| 极小值 |
| 1 |
所以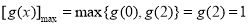 ,
,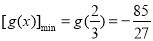 .
.
因为存在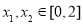 ,使得
,使得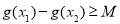 成立,
成立,
所以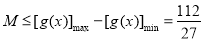 .所以实数M的最大值为
.所以实数M的最大值为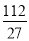 . 8分
. 8分
(3)由(2)知,在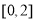 上,
上,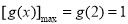 ,所以
,所以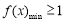 .
.
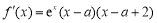 .
.
(ⅰ)当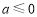 或
或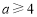 时,在
时,在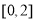 上,
上,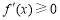 ,
,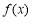 是单调增函数.
是单调增函数.
所以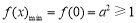 ,解得
,解得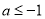 或
或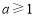 .所以
.所以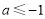 或
或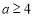 .
.
(ⅱ)当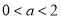 时,在
时,在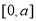 上,
上,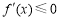 ,
,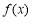 是单调减函数;
是单调减函数;
在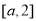 上,
上,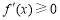 ,
,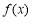 是单调增函数.所以
是单调增函数.所以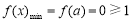 ,不成立.
,不成立.
(ⅲ)当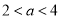 时,在
时,在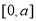 上,
上,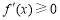 ,
,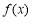 是单调增函数;
是单调增函数;
在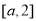 上,
上,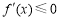 ,
,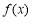 是单调减函数.
是单调减函数.
所以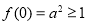 且
且 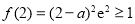 ,又
,又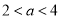 ,可得
,可得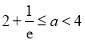 .
.
(ⅳ)当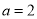 时,在
时,在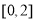 上,
上,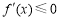 ,
,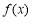 是单调减函数.
是单调减函数.
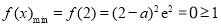 ,不成立.
,不成立.
综上,实数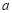 的取值范围是
的取值范围是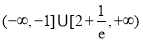 . 16分
. 16分
考点:(1)导数的几何意义;(2)利用导函数求函数的最值;(3)分类讨论思想的应用。


科目:高中数学 来源:2015届江西省南昌市三校高三10月联考理科数学试卷(解析版) 题型:选择题
已知△ABC的三内角A, B, C所对边的长依次为a,b,c,M为该三角形所在平面内的一点,若a +b
+b +c
+c =
= ,则M是△ABC的( )
,则M是△ABC的( )
A.内心 B.重心 C.垂心 D.外心
查看答案和解析>>
科目:高中数学 来源:2015届江西省高三上学期第三次考试文科数学试卷(解析版) 题型:选择题
设函数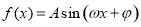
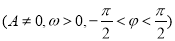 的图像关于直线
的图像关于直线 对称,它的周期是
对称,它的周期是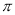 ,则
,则
A.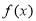 的图象过点
的图象过点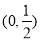
B.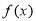 在
在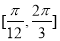 上是减函数
上是减函数
C.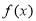 的一个对称中心是
的一个对称中心是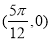
D.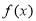 的最大值是A
的最大值是A
查看答案和解析>>
科目:高中数学 来源:2015届江苏省连云港高二下学期期末数学试卷(选修物理)(解析版) 题型:填空题
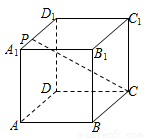
如图,已知点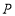 是正方体
是正方体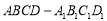 的棱
的棱 上的一个动点,设异面直线
上的一个动点,设异面直线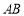 与
与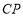 所成的角为
所成的角为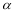 ,则
,则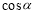 的最小值是 .
的最小值是 .
查看答案和解析>>
科目:高中数学 来源:2015届江苏省连云港高二下学期期末数学试卷(选修历史)(解析版) 题型:填空题
集合 中,每两个相异数作乘积,将所有这些乘积的和记为
中,每两个相异数作乘积,将所有这些乘积的和记为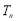 ,如:
,如:
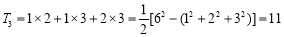 ;
;
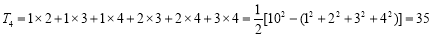 ;
;
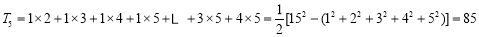
则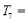 .(写出计算结果)
.(写出计算结果)
查看答案和解析>>
科目:高中数学 来源:2015届广东省深圳市高三上学期第一次五校联考文科数学试卷(解析版) 题型:解答题
某中学高三年级从甲(文)、乙(理)两个年级组各选出7名学生参加高校自主招生数学选拔考试,他们取得的成绩(满分100分)的茎叶图如图所示,其中甲组学生的平均分是85,乙组学生成绩的中位数是83.
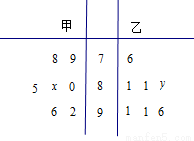
(1)求 和
和 的值;
的值;
(2)计算甲组7位学生成绩的方差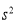 ;
;
(3)从成绩在90分以上的学生中随机抽取两名学生,求甲组至少有一名学生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com