
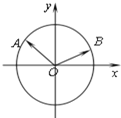
 如图,点A、B分别是角α、β的终边与单位圆的交点,0<β<$\frac{π}{2}$<α<π
如图,点A、B分别是角α、β的终边与单位圆的交点,0<β<$\frac{π}{2}$<α<π分析 (I)利用向量的数量积公式,即可证明;
(II)利用差角的余弦公式,再两边平方,即可得出结论.
解答 (I)证明:由题意得,$\overrightarrow{OA}$=(cosα,sinα),$\overrightarrow{OB}$=(cosβ,sinβ),
∴$\overrightarrow{OA}$•$\overrightarrow{OB}$=cosαcosβ+sinαsinβ …(2分)
又因为$\overrightarrow{OA}$与$\overrightarrow{OB}$夹角为α-β,|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=1,
∴$\overrightarrow{OA}$•$\overrightarrow{OB}$=|$\overrightarrow{OA}$||$\overrightarrow{OB}$|cos(α-β)=cos(α-β),…(4分)
综上cos(α-β)=cosαcosβ+sinαsinβ成立. …(6分)
(II)解:∵α=$\frac{3π}{4}$,cos(α-β)=$\frac{2}{3}$,∴-$\frac{\sqrt{2}}{2}$cosβ+$\frac{\sqrt{2}}{2}$sinβ=$\frac{2}{3}$,…(8分)
∴sinβ-cosβ=$\frac{2\sqrt{2}}{3}$,两边平方得,1-sin2β=$\frac{8}{9}$ …(10分)
∴sin2β=$\frac{1}{9}$. …(12分)
点评 本题考查差角的余弦公式的证明与运用,考查学生分析解决问题的能力,属于中档题.


 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:高中数学 来源: 题型:选择题
| A. | |b-a|≥1 | B. | 2a<2b | C. | lg$\frac{a}{b}$<0 | D. | 0<$\frac{b}{a}$<1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
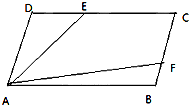 在平行四边形ABCD中,已知$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,E、F分别是边CD和BC上的点,满足$\overrightarrow{DC}$=3$\overrightarrow{DE}$,$\overrightarrow{BC}$=3$\overrightarrow{BF}$.
在平行四边形ABCD中,已知$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,E、F分别是边CD和BC上的点,满足$\overrightarrow{DC}$=3$\overrightarrow{DE}$,$\overrightarrow{BC}$=3$\overrightarrow{BF}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,抛物线C:x2=2py(p>0),其焦点为F,C上的一点M(4,m)满足|MF|=4.
如图所示,抛物线C:x2=2py(p>0),其焦点为F,C上的一点M(4,m)满足|MF|=4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|0≤x≤1} | B. | {x|1≤x<2} | C. | {x|-1<x≤0} | D. | {x|0≤x<1} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 直线和直线外一点确定一个平面 | |
| B. | 过不在一条直线上的三点,有且只有一个平面 | |
| C. | 空间中如果两个角的两边分别对应平行,那么这两个角相等或互补 | |
| D. | 平行于同一个平面的两个平面相互平行 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com