
| A. | n | B. | 2n | C. | n+2 | D. | 2n+2 |
分析 把已知的数列递推式变形,求得$\frac{{a}_{n+1}}{{a}_{n}}=\frac{n+1}{n}$,然后利用累积法得答案.
解答 解:由na${\;}_{n+1}^{2}$-anan+1=(n+1)a${\;}_{n}^{2}$,得$n•(\frac{{a}_{n+1}}{{a}_{n}})^{2}-\frac{{a}_{n+1}}{{a}_{n}}=n+1$,
∴$(\frac{{a}_{n+1}}{{a}_{n}}+1)(n\frac{{a}_{n+1}}{{a}_{n}}-n-1)=0$,
∵an>0,∴$\frac{{a}_{n+1}}{{a}_{n}}=\frac{n+1}{n}$.
∴${a}_{n}=\frac{{a}_{n}}{{a}_{n-1}}•\frac{{a}_{n-1}}{{a}_{n-2}}…\frac{{a}_{2}}{{a}_{1}}•{a}_{1}$=$\frac{n}{n-1}•\frac{n-1}{n-2}•…•\frac{2}{1}•1$=n.
故选:A.
点评 本题考查数列递推式,考查了累积法求数列的通项公式,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
 如图,在平面直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{2\sqrt{2}}{3}$,经过椭圆的左顶点A(-3,0)作斜率为k(k≠0)的直线l交椭圆C于点D,交轴于点E
如图,在平面直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{2\sqrt{2}}{3}$,经过椭圆的左顶点A(-3,0)作斜率为k(k≠0)的直线l交椭圆C于点D,交轴于点E查看答案和解析>>
科目:高中数学 来源: 题型:选择题
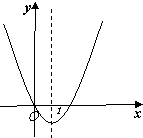 (文)二次函数y=x2+bx的图象如图,对称轴为x=1.若关于x的二次方程x2+bx-t=0(为实数)在-1<x<4的范围内有解,则t的取值范围是( )
(文)二次函数y=x2+bx的图象如图,对称轴为x=1.若关于x的二次方程x2+bx-t=0(为实数)在-1<x<4的范围内有解,则t的取值范围是( )| A. | -1≤t<3 | B. | t≥-1 | C. | 3<t<8 | D. | -1≤t<8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\frac{\sqrt{7}}{2}$ | C. | 2 | D. | $\sqrt{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
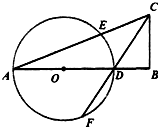 如图:已知直角三角形ABC,∠B为直角,∠C的平分线交AB于D,以AD为直径作圆O,交AC于点E,交CD于F.
如图:已知直角三角形ABC,∠B为直角,∠C的平分线交AB于D,以AD为直径作圆O,交AC于点E,交CD于F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com