
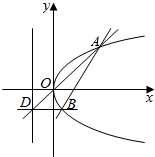
 已知斜率为1的直线l经过抛物线y2=2px(p>0)的焦点F,且与抛物线相交于A,B两点,|AB|=4.
已知斜率为1的直线l经过抛物线y2=2px(p>0)的焦点F,且与抛物线相交于A,B两点,|AB|=4.分析 (I)由$\left\{\begin{array}{l}y=x-\frac{p}{2}\\{y^2}=2px\end{array}\right.$消y并整理,利用|AB|=|AF|+|BF|=x1+x2+p=4,求p的值;
(Ⅱ)写出点A、B、D的坐标,可利用斜率相等,证明三点共线.
解答 解:(I)由题意可知,抛物线y2=2px(p>0)的焦点坐标为$F(\frac{p}{2},0)$,
准线方程为$x=-\frac{p}{2}$.
所以,直线l的方程为$y=x-\frac{p}{2}$…(2分)
由$\left\{\begin{array}{l}y=x-\frac{p}{2}\\{y^2}=2px\end{array}\right.$消y并整理,得${x^2}-3px+\frac{p^2}{4}=0$…(3分)
设A(x1,y1),B(x2,y2)
则x1+x2=3p,
又|AB|=|AF|+|BF|=x1+x2+p=4,
所以,3p+p=4,p=1…(6分)
(II)由(I)可知,抛物线的方程为y2=2x.
设点B的坐标为$(\frac{{{y_0}^2}}{2},{y_0})$,又焦点$F(\frac{1}{2},0)$,
当$\frac{{{y_0}^2}}{2}≠\frac{1}{2}$时,直线AB的斜率为$k=\frac{{{y_0}-0}}{{\frac{{{y_0}^2}}{2}-\frac{1}{2}}}=\frac{{2{y_0}}}{{{y^2}_0-1}}$.
所以,直线AB的方程为$y-0=\frac{{2{y_0}}}{{{y_0}^2-1}}(x-\frac{1}{2})$,即$y=\frac{{2{y_0}}}{{{y_0}^2-1}}x-\frac{y_0}{{{y_0}^2-1}}$…(9分)
由$\left\{\begin{array}{l}y=\frac{{2{y_0}}}{{{y_0}^2-1}}x-\frac{y_0}{{{y_0}^2-1}}\\{y^2}=2x\end{array}\right.$消x并整理,得${y^2}-\frac{{{y_0}^2-1}}{y_0}y-1=0$
所以,y1y2=-1
又y2=y0,所以,${y_1}=-\frac{1}{y_0}$,${x_1}=\frac{1}{{2{y_0}^2}}$即$A(\frac{1}{{2{y_0}^2}},-\frac{1}{y_0})$.…(11分)
由题意可知,点D的坐标为$(-\frac{1}{2},{y_0})$,
所以,OA的斜率为${k_{OA}}=\frac{{-\frac{1}{y_0}}}{{\frac{1}{{2{y_0}^2}}}}=-2{y_0}$,OD的斜率为${k_{OD}}=\frac{y_0}{{-\frac{1}{2}}}=-2{y_0}$,即kOA=kOD
所以,A,O,D三点共线.…(13分)
当$\frac{{{y_0}^2}}{2}=\frac{1}{2}$时,|AB|=2不合题意,舍去.…(14分)
点评 本题考查抛物线的方程与性质,考查三点共线的证明,涉及分类讨论的思想,属中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | $\frac{1}{4}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 32 | B. | 33 | C. | 34 | D. | 35 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com