练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．已知直线x-y+a=0与圆心为C的圆x2+y2+2x-4y-4=0相交于A，B两点，且AC⊥BC，求实数a的值．

    分析 根据圆的标准方程，求出圆心和半径，根据点到直线的距离公式即可得到结论．

    解答 解：圆的标准方程为（x+1）2+（y-2）2=9，圆心C（-1，2），半径r=3，
    ∵AC⊥BC，
    ∴圆心C到直线AB的距离d=$\frac{3\sqrt{2}}{2}$，
    即d=$\frac{|-1-2+a|}{\sqrt{2}}$=$\frac{3\sqrt{2}}{2}$，
    即|a-3|=3，
    解得a=0或a=6．

    点评 本题主要考查点到直线的距离公式的应用，利用条件求出圆心和半径，结合距离公式是解决本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    8．已知极坐标系的极点与直角坐标系的原点重合，极轴与x轴的非负半轴重合，曲线C的极坐标方程为：ρsin2θ=4cosθ，曲线D的参数方程为$\left\{\begin{array}{l}{x=t+2}\\{y=2t-5}\end{array}\right.$（t为参数）
    （1）将曲线C的极坐标方程化为直角坐标方程，将曲线D的参数方程化为普通方程；
    （2）设曲线C与曲线D交于A，B，求向量$\overrightarrow{OA}$•$\overrightarrow{OB}$．．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．设$n=\int_0^{\frac{π}{2}}{4sinxdx}$，则二项式${（{x-\frac{2}{x}}）^n}$的展开式的常数项是24．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．如图，茎叶图记录了某校“春季运动会”甲、乙两名运动员的成绩，他们的平均成绩均为82分，则x+y=（　　）
    A．4B．5C．6D．7

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．点P（0，4）关于x-y+3=0的对称点Q在直线l上，且l与直线3x-y+2=0平行
    （1）求直线l的方程
    （2）求圆心在直线l上，与x轴相切，且被直线x-2y=0截得的弦长为4的圆的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

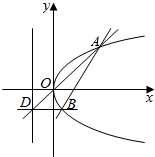    3．已知斜率为1的直线l经过抛物线y2=2px（p＞0）的焦点F，且与抛物线相交于A，B两点，|AB|=4．
    （I）求p的值；
    （Ⅱ）设经过点B和抛物线对称轴平行的直线交抛物线y2=2px的准线于点D，求证：A，O，D三点共线（O为坐标原点）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

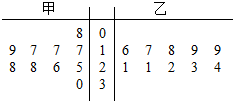    10．某校为了解高三学生英语听力情况，抽查了甲、乙两班各十名学生的一次英语听力成绩，并将所得数据用茎叶图表示（如图所示），则以下判断正确的是（　　）
    A．甲组数据的众数为28B．甲组数据的中位数是22
    C．乙组数据的最大值为30D．乙组数据的极差为16

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．PM2.5是指空气中直径小于或等于2.5微米的颗粒物（也称可入肺颗粒物）．为了探究车流量与PM2.5的浓度是否相关，现采集到某城市周一至周五某一时间段车流量与PM2.5得数据如下表：
    时间周一周二周三周四周五
    车流量x（万辆）5051545758
    PM2.5的浓度y（微克/立方米）6970747879
    （Ⅰ）根据上表数据求出y与x的线性回归直线方程$\hat y=\hat bx+\hat a$，
    （Ⅱ）若周六同一时间段车流量是25万辆，试根据（Ⅰ）中求出的线性回归方程预测此时PM2.5的浓度是多少？（保留整数）
    参考公式其中$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$：方程$\hat y=\hat bx+\hat a$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．下列函数中，在区间（0，+∞）上为增函数的是（　　）
    A．y=$\frac{1}{x}$B．y=-x2C．y=（$\frac{1}{2}$）xD．y=log2x

    查看答案和解析>>

    同步练习册答案