
直线y=kx+b与曲线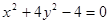 交于A、B两点,记△AOB的面积为S(O是坐标原点).
交于A、B两点,记△AOB的面积为S(O是坐标原点).
(1)求曲线的离心率;
(2)求在k=0,0<b<1的条件下,S的最大值;
(3)当|AB|=2,S=1时,求直线AB的方程.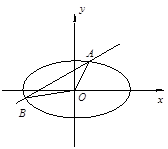
(1)离心率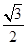 .(2)当
.(2)当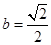 时, S取到最大值1.
时, S取到最大值1.
(3)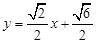 或
或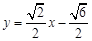 或
或 或
或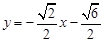 .
.
解析试题分析:(1)转化成标准方程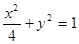 ,明确曲线为椭圆,
,明确曲线为椭圆,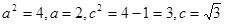 ,进一步得到椭圆的离心率.
,进一步得到椭圆的离心率.
(2)设点A的坐标为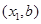 ,点B的坐标为
,点B的坐标为 ,由
,由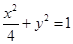 ,解得
,解得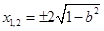 ,
,
将面积用b表示.
(3)由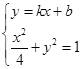 ,应用弦长公式,得到|AB|=
,应用弦长公式,得到|AB|=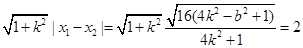 ,
,
根据O到AB的距离得到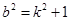 代入上式并整理,解得k,b.
代入上式并整理,解得k,b.
试题解析: (1)曲线的方程可化为: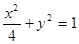 ,
,
∴此曲线为椭圆,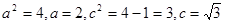 ,
,
∴此椭圆的离心率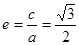 . 4分
. 4分
(2)设点A的坐标为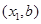 ,点B的坐标为
,点B的坐标为 ,
,
由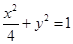 ,解得
,解得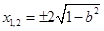 , 6分
, 6分
所以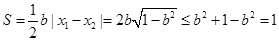
当且仅当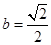 时, S取到最大值1. 8分
时, S取到最大值1. 8分
(3)由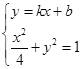 得
得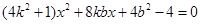 ,
, 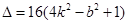 ①
①
|AB|=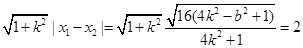 ②
②
又因为O到AB的距离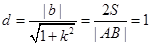 ,所以
,所以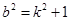 ③
③
③代入②并整理,得
解得,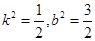 ,代入①式检验,△>0 ,
,代入①式检验,△>0 ,
故直线AB的方程是 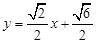 或
或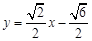 或
或 或
或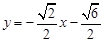 . 14分
. 14分
考点:椭圆的几何性质,直线与椭圆的位置关系,点到直线的距离公式,函数的最值.


科目:高中数学 来源: 题型:解答题
如图,在平面直角坐标系 中,
中,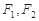 分别是椭圆
分别是椭圆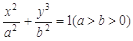 的左、右焦点,顶点
的左、右焦点,顶点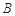 的坐标为
的坐标为 ,连结
,连结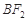 并延长交椭圆于点A,过点A作
并延长交椭圆于点A,过点A作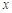 轴的垂线交椭圆于另一点C,连结
轴的垂线交椭圆于另一点C,连结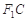 .
.
(1)若点C的坐标为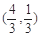 ,且
,且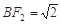 ,求椭圆的方程;
,求椭圆的方程;
(2)若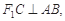 求椭圆离心率e的值.
求椭圆离心率e的值.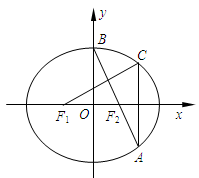
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知椭圆C: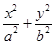 =1(a>0,b>0)的离心率与双曲线
=1(a>0,b>0)的离心率与双曲线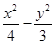 =1的一条渐近线的斜率相等以原点为圆心,椭圆的短半轴长为半径的圆与直线sin
=1的一条渐近线的斜率相等以原点为圆心,椭圆的短半轴长为半径的圆与直线sin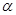 ·x+cos
·x+cos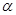 ·y-l=0相切(
·y-l=0相切(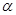 为常数).
为常数).
(1)求椭圆C的方程;
(2)若过点M(3,0)的直线与椭圆C相交TA,B两点,设P为椭圆上一点,且满足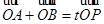 (O为坐标原点),当
(O为坐标原点),当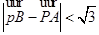 时,求实数t取值范围.
时,求实数t取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,矩形ABCD中,|AB|=4,|BC|=2,E,F,M,N分别是矩形四条边的中点,G,H分别是线段ON,CN的中点.
(1)证明:直线EG与FH的交点L在椭圆W: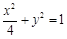 上;
上;
(2)设直线l: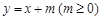 与椭圆W:
与椭圆W: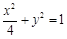 有两个不同的交点P,Q,直线l与矩形ABCD有两个不同的交点S,T,求
有两个不同的交点P,Q,直线l与矩形ABCD有两个不同的交点S,T,求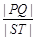 的最大值及取得最大值时m的值.
的最大值及取得最大值时m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知⊙O′过定点A(0,p)(p>0),圆心O′在抛物线C:x2=2py(p>0)上运动,MN为圆O′在x轴上所截得的弦.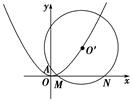
(1)当O′点运动时,|MN|是否有变化?并证明你的结论;
(2)当|OA|是|OM|与|ON|的等差中项时,试判断抛物线C的准线与圆O′的位置关系,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分13分)
如图,已知抛物线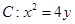 ,过点
,过点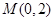 任作一直线与
任作一直线与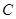 相交于
相交于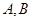 两点,过点
两点,过点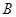 作
作 轴的平行线与直线
轴的平行线与直线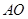 相交于点
相交于点 (
(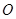 为坐标原点).
为坐标原点).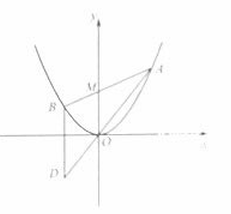
(1)证明:动点 在定直线上;
在定直线上;
(2)作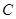 的任意一条切线
的任意一条切线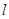 (不含
(不含 轴)与直线
轴)与直线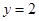 相交于点
相交于点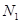 ,与(1)中的定直线相交于点
,与(1)中的定直线相交于点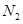 ,证明:
,证明: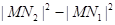 为定值,并求此定值.
为定值,并求此定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com