
分析 (1)由于l1⊥l2,所以△ABD是直角三角形,△ABD外接圆圆心直径是AB,|AB|2=8(m2+1),所以外接圆C面积的最小值为2π;
(2)假设存在点P(x0,y0)满足条件,则${x_0}^2=2{y_0}$,分当DE是底时,当PE是底时,当PD是底时,分别求出相应的点的个数,问题得以解决.
解答 解:(Ⅰ)由于l1⊥l2,所以△ABD是直角三角形,
A(0,2m+2),B(2-2m,0),D(2,2),
则△ABD外接圆圆心直径是AB,|AB|2=8(m2+1),
要使△ABD外接圆C面积最小,则|AB|2min=8,当且仅当m=0时成立,
所以外接圆C面积的最小值为2π.
(Ⅱ)由D(2,2)点在抛物线x2=2py上,则x2=2y,
圆C过原点,则抛物线与圆的公共点是D(2,2),E(0,0),
假设存在点P(x0,y0)满足条件,则${x_0}^2=2{y_0}$,
(1)当DE是底时,DE中点Q(1,1),DE中垂线方程:y=-x+2,代入抛物线x2=2y
得:x2+2x-4=0,△=20>0,所以存在两个满足条件的P点.
(2)当PE是底时,PE中点M$(\frac{x_0}{2},\frac{y_0}{2})$,则DM⊥PE,
即${x_0}(\frac{x_0}{2}-2)+{y_0}(\frac{y_0}{2}-2)=0,{x_0}^3-4{x_0}-16=0$,
设f(x)=x3-4x-16,f'(x)=3x2-4,
则f(x)在$(-∞,-\frac{{2\sqrt{3}}}{3})$,$(\frac{{2\sqrt{3}}}{3},+∞)$递增,在$(-\frac{{2\sqrt{3}}}{3},\frac{{2\sqrt{3}}}{3})$递减,
因为$f(-\frac{{2\sqrt{3}}}{3})<0,f(0)=-16<0$,f(3)=-1<0,f(4)=32>0,
所以f(x)在(3,4)有唯一零点,存在一个满足条件的P点.
(3)当PD是底时,PD中点N$(\frac{x_0}{2}+1,\frac{y_0}{2}+1)$,
则EN⊥PD,$\overrightarrow{EN}=(\frac{x_0}{2}+1,\frac{y_0}{2}+1)$,$\overrightarrow{DP}=({x_0}-2,{y_0}-2)$,$\overrightarrow{EN}•\overrightarrow{DP}=0$,
即$(\frac{{{x_0}+2}}{2})({x_0}-2)+(\frac{{{y_0}+2}}{2})({y_0}-2)=0$,
所以$(\frac{{{x_0}^2-4}}{2})+(\frac{{{x_0}^2+4}}{4})(\frac{{{x_0}^2-4}}{2})=0$,则${x_0}^2-4=0$或${x_0}^2+8=0$,
只有1解x0=-2.
综上所述:以上零点不重复,共有4个满足条件的P点.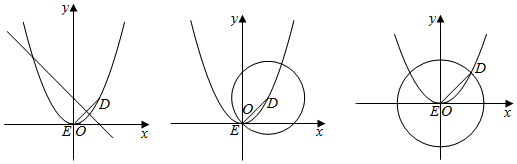
说明:
若只画出以上三图,说明DE作为底或腰的等腰三角形有4个,最多给(2分),若不完整给(1分);若只有结果4个等腰三角形,给(1分).
点评 本小题考查对含参直线方程的理解,抛物线的基础知识,探究存在性问题,考查学生的数学思维能力及逻辑运算能力,考查数形结合、函数方程、分类与整合的数学思想.


科目:高中数学 来源: 题型:选择题
| A. | (-∞,-$\frac{1}{2}$) | B. | (-∞,-$\frac{5}{4}$) | C. | [-$\frac{5}{4}$,+∞) | D. | [-$\frac{5}{4}$,-$\frac{1}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 等腰直角三角形 | B. | 直角三角形 | ||
| C. | 等腰三角形 | D. | 等腰或直角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,π) | B. | (0,π] | C. | (0,4π) | D. | (0,4π] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
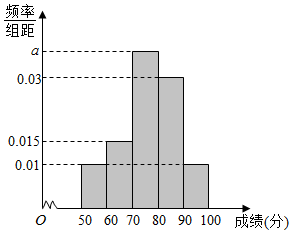 100名学生某次数学考试成绩(单位:分)的频率分布直方图如图所示.
100名学生某次数学考试成绩(单位:分)的频率分布直方图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com