
分析 (1)利用数列的前n项和与第n项的关系,得到关于数列的递推关系式,即可求得S1,S2,S3,S4.
(2)用数学归纳法证明数列问题时分为两个步骤,第一步,先证明当n=1时,结论显然成立,第二步,先假设当n=k+1时,有Sk=$\frac{k}{2k+1}$,利用此假设证明当n=k+1时,结论也成立即可
解答 解:(1)S1=a1=$\frac{1}{3}$,
S2=(2×4-2)(S2-S1),∴S2=$\frac{2}{5}$,
S3=(2×9-3)(S3-S2),∴S3=$\frac{3}{7}$,
S4=(2×16-4)(S4-S3),∴S4=$\frac{4}{9}$
(2)由(1)的计算可猜想Sn=$\frac{n}{2n+1}$,
下面用数学归纳法证
①当n=1时,结论显然成立.
②假设当n=k时结论成立,即Sk=$\frac{k}{2k+1}$,
则当n=k+1时,Sk+1=[2×(k+1)2-(k+1)](Sk+1-Sk),
∴(2k2+3k)Sk+1=k(k+1),
∴Sk+1=$\frac{k+1}{2k+3}$=$\frac{k+1}{2(k+1)+1}$,
故当n=k+1时结论也成立.
由①、②可知,对于任意的n∈N*,都有Sn=$\frac{n}{2n+1}$.
点评 本题主要考查数列递推式、数学归纳法,第(1)问要注意递推公式的灵活运用,第(2)问要注意数学归纳法的证明技巧.数学归纳法的基本形式设P(n)是关于自然数n的命题,若1°P(n0)成立2°假设P(k)成立(k≥n0),可以推出P(k+1)成立,则P(n)对一切大于等于n0的自然数n都成立.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:解答题
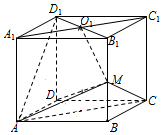 如图,直四棱柱ABCD-A1B1C1D1的棱长均为2,∠BAD=60°,M为BB1的中点,Ol为上底面对角线的交点.
如图,直四棱柱ABCD-A1B1C1D1的棱长均为2,∠BAD=60°,M为BB1的中点,Ol为上底面对角线的交点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a,b,c中至多有一个偶数 | B. | a,b,c中一个偶数都没有 | ||
| C. | a,b,c至多有一个奇数 | D. | a,b,c都是偶数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{1}{2}$个单位长度 | B. | 向右平移$\frac{1}{2}$个单位长度 | ||
| C. | 向左平移$\frac{π}{6}$个单位长度 | D. | 向右平移$\frac{π}{6}$个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{8}$个单位 | B. | 向右平移$\frac{π}{8}$个单位 | ||
| C. | 向左平移$\frac{π}{4}$个单 | D. | 向右平移$\frac{π}{4}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
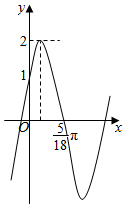 函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com