
 如表中给出了2011年~2015年某市快递业务总量的统计数据(单位:百万件)
如表中给出了2011年~2015年某市快递业务总量的统计数据(单位:百万件)| 年份 | 2011 | 2012 | 2013 | 2014 | 2015 |
| 年份代码 | 1 | 2 | 3 | 4 | 5 |
| 快递业务总量 | 34 | 55 | 71 | 85 | 105 |
分析 (Ⅰ)根据表中所给的数据,得到点的坐标,在平面直角坐标系中画出散点图;
(Ⅱ)先求出年份代码x和快递量y的平均数,得到这组数据的样本中心点,利用最小二乘法求出线性回归方程的系数,代入样本中心点求出a的值,写出线性回归方程;
(Ⅲ)先求得2016年对于的年份代码,代入线性回归方程,即可求得该市2016年的快递业务总量.
解答 解:(Ⅰ)所给数据的折线图如下: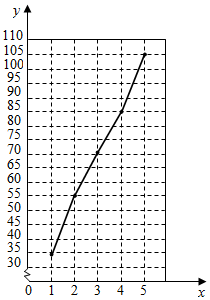
…(3分)
(Ⅱ)可得$\overline x=3$,$\overline y=70$,
$\widehatb=\frac{(1-3)(34-70)+(2-3)(55-70)+(3-3)(71-70)+(4-3)(85-70)+(5-3)(105-70)}{{{{(1-3)}^2}+{{(2-3)}^2}+{{(3-3)}^2}+{{(4-3)}^2}+{{(5-3)}^2}}}$,
=$\frac{72+15+0+15+70}{4+1+0+1+4}=\frac{172}{10}=17.2$,$\widehata=70-17.2×3=18.4$,
∴y与x的回归模型为:$\widehaty=17.2x+18.4$.…(9分)
(Ⅲ)把2016年的年份代码x=6代入回归模型得$\widehaty=17.2×6+18.4=121.6$(百万件),
∴预计该市2016年的快递业务总量约为121.6百万件.…(12分)
点评 本题考查散点图,考查线性回归方程的求法,考查利用线性回归方程进行预测,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}+\sqrt{6}}{2}$ | B. | $\frac{\sqrt{2}-\sqrt{6}}{2}$ | C. | $\frac{\sqrt{2}+\sqrt{6}}{4}$ | D. | $\frac{\sqrt{2}-\sqrt{6}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
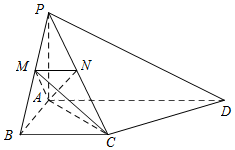 如图,PA⊥平面ABCD,AB⊥AD,AD∥BC,PA=AB=BC,AD=2AB,点M,N分别在PB,PC上,且MN∥BC.
如图,PA⊥平面ABCD,AB⊥AD,AD∥BC,PA=AB=BC,AD=2AB,点M,N分别在PB,PC上,且MN∥BC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{3}$个单位长度 | B. | 向右平移$\frac{π}{3}$个单位长度 | ||
| C. | 向左平移$\frac{2π}{3}$个单位长度 | D. | 向右平移$\frac{2π}{3}$个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com