
科目:高中数学 来源:2016届河北省高三上学期四调文科数学试卷(解析版) 题型:解答题
(本题小满分12分)
如图,直三棱柱 中,
中, ,
, 分别是
分别是 ,
, 的中点,
的中点, .
.
(1)证明: 平面
平面 ;
;
(2)求异面直线 和
和 所成角的大小;
所成角的大小;
(3)当 时,求三棱锥
时,求三棱锥 的体积.
的体积.

查看答案和解析>>
科目:高中数学 来源:2016届湖北武汉华中师大一附等高三上第一次联考文数学卷(解析版) 题型:解答题
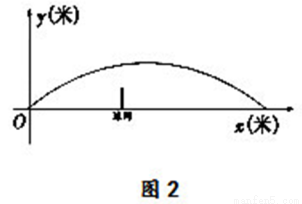
小明同学制作了一个简易的网球发射器,可用于帮忙练习定点接发球,如图1所示,网球场前半区、后半区总长为23.77米,球网的中间部分高度为0.914米,发射器固定安装在后半区离球网底部8米处中轴线上,发射方向与球网底部所在直线垂直.为计算方便,球场长度和球网中间高度分别按24米和1米计算,发射器和网球大小均忽略不计.如图2所示,以发射器所在位置为坐标原点建立平面直角坐标系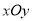 ,
,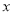 轴在地平面上的球场中轴线上,
轴在地平面上的球场中轴线上,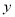 轴垂直于地平面,单位长度为1米.已知若不考虑球网的影响,网球发射后的轨迹在方程
轴垂直于地平面,单位长度为1米.已知若不考虑球网的影响,网球发射后的轨迹在方程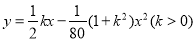 表示的曲线上,其中
表示的曲线上,其中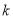 与发射方向有关.发射器的射程是指网球落地点的横坐标.
与发射方向有关.发射器的射程是指网球落地点的横坐标.
(1)求发射器的最大射程;
(2)请计算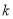 在什么范围内,发射器能将球发过网(即网球飞行到球网正上空时,网球离地距离大于1米)?若发射器将网球发过球网后,在网球着地前,小明要想在前半区中轴线的正上空选择一个离地面2.55米处的击球点正好击中网球,试问击球点的横坐标
在什么范围内,发射器能将球发过网(即网球飞行到球网正上空时,网球离地距离大于1米)?若发射器将网球发过球网后,在网球着地前,小明要想在前半区中轴线的正上空选择一个离地面2.55米处的击球点正好击中网球,试问击球点的横坐标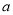 最大为多少?并请说明理由.
最大为多少?并请说明理由.
查看答案和解析>>
科目:高中数学 来源:2016届湖北武汉华中师大一附等高三上第一次联考理数学卷(解析版) 题型:解答题
如图, 中,三个内角
中,三个内角 、
、 、
、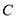 成等差数列,且
成等差数列,且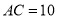 ,
, .
.

(1)求 的面积;
的面积;
(2)已知平面直角坐标系 ,点
,点 ,若函数
,若函数
 的图象经过
的图象经过 、
、 、
、 三点,且
三点,且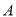 、
、 为
为 的图象与
的图象与 轴相邻的两个交点,求
轴相邻的两个交点,求 的解析式.
的解析式.
查看答案和解析>>
科目:高中数学 来源:2015-2016学年浙江省高一上学期期中数学试卷(解析版) 题型:解答题
已知函数 ,
,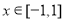 .
.
(1)求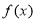 的最小值(用
的最小值(用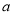 表示);
表示);
(2)关于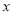 的方程
的方程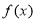
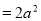 有解,求实数
有解,求实数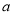 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2016届甘肃省高三12月月考理科数学试卷(解析版) 题型:解答题
如图,在四棱锥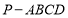 中,底面
中,底面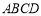 为直角梯形,AD‖BC,
为直角梯形,AD‖BC, 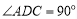 ,平面
,平面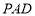 ⊥底面
⊥底面 ,Q为AD的中点,M是棱PC上的点,PA=PD=AD=2,BC=1,CD=
,Q为AD的中点,M是棱PC上的点,PA=PD=AD=2,BC=1,CD=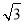 .
.
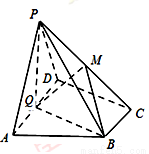
(Ⅰ)求证:平面PQB⊥平面PAD;
(Ⅱ)若二面角M-BQ-C为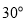 ,设PM=t
,设PM=t MC,试确定t的值.
MC,试确定t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com