
【题目】已知函数f(x)=log2(2x+1)﹣ ![]() .
.
(1)证明:对任意的b∈R,函数f(x)=log2(2x+1)﹣ ![]() 的图象与直线y=
的图象与直线y= ![]() +b最多有一个交点;
+b最多有一个交点;
(2)设函数g(x)=log4(a﹣2x),若函数y=f(x)与函数y=g(x)的图象至少有一个交点,求实数a的取值范围.
【答案】
(1)证明:原问题等价于log2(2x+1)﹣ ![]() =
= ![]() +b解的讨论.
+b解的讨论.
因为2x+1=2x+b,即2x(2b﹣1)=1.
当b≤0时,方程无解,即两图象无交点;
当b>0时,方程有一解,即两图象有一个交点,得证
(2)解:函数y=f(x)与函数y=g(x)的图象至少有一个交点,
等价于方程log2(2x+1)﹣ ![]() =log4(a﹣2x)至少有一个解,
=log4(a﹣2x)至少有一个解,
即(2x+1)2=2x(a﹣2x).
设u=2x>0,即方程2u2+(2﹣a)u+1=0至少有一个正解.
①当△=(2﹣a)2﹣8=0时,即a=2±2 ![]() ,
,
∵a>2x>0,
∴a=2﹣2 ![]() 不符合题意,
不符合题意,
当a=2+2 ![]() 时,方程有一个正解,符合题意.
时,方程有一个正解,符合题意.
②当 ![]() 时,即a>2+2
时,即a>2+2 ![]() ,此时方程有两个不同的正解.
,此时方程有两个不同的正解.
综上所述:实数a的取值范围是[2+2 ![]() ,+∞)
,+∞)
【解析】(1)问题等价于log2(2x+1)﹣ ![]() =
= ![]() +b解的讨论,通过讨论b的范围,证明即可;(2)等价于方程log2(2x+1)﹣
+b解的讨论,通过讨论b的范围,证明即可;(2)等价于方程log2(2x+1)﹣ ![]() =log4(a﹣2x)至少有一个解,即(2x+1)2=2x(a﹣2x),通过讨论判别式△,求出a的范围即可.
=log4(a﹣2x)至少有一个解,即(2x+1)2=2x(a﹣2x),通过讨论判别式△,求出a的范围即可.
【考点精析】掌握复合函数单调性的判断方法是解答本题的根本,需要知道复合函数f[g(x)]的单调性与构成它的函数u=g(x),y=f(u)的单调性密切相关,其规律:“同增异减”.


科目:高中数学 来源: 题型:
【题目】数列{an}的前n项和为Sn , a1=1,an+1=2Sn(n∈N*).
(Ⅰ)求数列{an}的通项an;
(Ⅱ)求数列{nan}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在三棱锥S﹣ABC中,SO⊥平面ABC,侧面SAB与SAC均为等边三角形,∠BAC=90°,O为BC的中点,求二面角A﹣SC﹣B的余弦值. 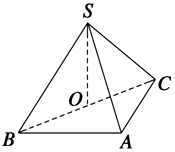
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加高三模拟考试的学生中随机抽取60名学生,按其数学成绩(均为整数)分成六组![]() 后得到如右部分频率分布直方图,观察图中的信息,
后得到如右部分频率分布直方图,观察图中的信息,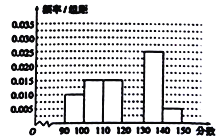
回答下列问题:
(1)补全频率分布直方图;并估计本次考试的数学平均成绩(同一组中的数据用该组区间的中点值作代表);
(2)用分层抽样的方法在分数段为![]() 的学生成绩中抽取一个容量为6的样本,再从这6个样本中任取2人成绩,求至多有1人成绩在分数段
的学生成绩中抽取一个容量为6的样本,再从这6个样本中任取2人成绩,求至多有1人成绩在分数段![]() 内的概率.
内的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com