练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】若函数y=x2﹣3x﹣4的定义域为[0，m]，值域为 ，则m的取值范围是（ ）
    A.（0，4]
    B.
    C.
    D.

    【答案】C
    【解析】解：y=x2﹣3x﹣4=x2﹣3x+ ﹣ =（x﹣ ）2﹣
    定义域为〔0，m〕
    那么在x=0时函数值最大
    即y最大=（0﹣ ）2﹣ = ﹣ =﹣4
    又值域为〔﹣ ，﹣4〕
    即当x=m时，函数最小且y最小=﹣
    即﹣ ≤（m﹣ ）2﹣ ≤﹣4
    0≤（m﹣ ）2≤
    即m≥ （1）
    即（m﹣ ）2≤
    m﹣ ≥﹣3 且m﹣ ≤
    0≤m≤3 （2）
    所以： ≤m≤3
    故选C．
    【考点精析】掌握函数的定义域及其求法和函数的值域是解答本题的根本，需要知道求函数的定义域时，一般遵循以下原则：①是整式时，定义域是全体实数;②是分式函数时，定义域是使分母不为零的一切实数;③是偶次根式时，定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零，当对数或指数函数的底数中含变量时，底数须大于零且不等于1,零（负）指数幂的底数不能为零；求函数值域的方法和求函数最值的常用方法基本上是相同的．事实上，如果在函数的值域中存在一个最小（大）数，这个数就是函数的最小（大）值．因此求函数的最值与值域，其实质是相同的．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=log2（2x+1）﹣ ．
    （1）证明：对任意的b∈R，函数f（x）=log2（2x+1）﹣ 的图象与直线y= +b最多有一个交点；
    （2）设函数g（x）=log4（a﹣2x），若函数y=f（x）与函数y=g（x）的图象至少有一个交点，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知关于x的函数y= （t∈R）的定义域为D，存在区间[a，b]D，f（x）的值域也是[a，b]．当t变化时，b﹣a的最大值= ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=cos2x﹣ sinxcosx+1．
    （1）求函数f（x）的单调递增区间；
    （2）若f（θ）= ，θ∈（ ， ），求sin2θ的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=Asin（ωx+φ）+B（A＞0，ω＞0，|φ|＜ ）的最小正周期为2 π，最小值为﹣2，且当x= 时，函数取得最大值4． （I）求函数 f（x）的解析式；
    （Ⅱ）求函数f（x）的单调递增区间；
    （Ⅲ）若当x∈[ ， ]时，方程f（x）=m+1有解，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在区间D上，若函数y=f（x）为增函数，而函数 为减函数，则称函数y=f（x）为区间D上的“弱增”函数．则下列函数中，在区间[1，2]上不是“弱增”函数的为（ ）
    A.
    B.
    C.g（x）=x2+1
    D.g（x）=x2+4

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，△ABC中，已知顶点A（3，﹣1），∠B的内角平分线方程是x﹣4y+10=0过点C的中线方程为6x+10y﹣59=0．求顶点B的坐标和直线BC的方程．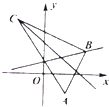

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知△ABC中，内角A，B，C所对的边分别为，b，c，且acosC+ c=b，若a=1， c﹣2b=1，则角C为（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}： ， + ， + + ， + + + ，…，那么数列{bn}={ }的前n项和为（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    同步练习册答案