
分析 (1)由函数性质能求出f(2),f($\frac{1}{2}$),f[f(-1)];
(2)当a≤1时,f(a)=a+2=3;当-1<a<2时,f(a)=a2=3;当a≥2时,f(a)=2a=3.由此能求出a的值.
解答 解:(1)∵函数f(x)=$\left\{\begin{array}{l}{x+2(x≤-1)}\\{{x}^{2}(-1<x<2)}\\{2x(x≥2)}\end{array}\right.$
∴f(2)=2×2=4,
f($\frac{1}{2}$)=($\frac{1}{2}$)2=$\frac{1}{4}$,
f(-1)=-1+2=1,
f[f(-1)]=f(1)=12=1.
(2)当a≤1时,f(a)=a+2=3,解得a=1,成立;
当-1<a<2时,f(a)=a2=3,解得a=$\sqrt{3}$或a=-$\sqrt{3}$(舍);
当a≥2时,f(a)=2a=3,解得a=$\frac{3}{2}$,不成立.
∴a的值为1或$\sqrt{3}$.
点评 本题考查函数值的求法,考查实数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
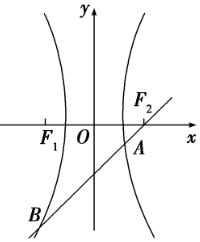 过双曲线$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1的右焦点作倾斜角为45°的弦AB.求:
过双曲线$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1的右焦点作倾斜角为45°的弦AB.求:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | .6 | B. | 8 | C. | 10 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在正四棱锥P-AMDE,底面AMDE的边长为2,侧棱PA=$\sqrt{5}$,B,C分别
如图,在正四棱锥P-AMDE,底面AMDE的边长为2,侧棱PA=$\sqrt{5}$,B,C分别查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com