
| A�� | $��k��+\frac{��}{12}��k��+\frac{5��}{12}����k��Z$ | B�� | $��k��+\frac{5��}{12}��k��+\frac{3��}{4}����k��Z$ | ||
| C�� | $��k��-\frac{7��}{12}��k��+\frac{��}{12}����k��Z$ | D�� | $��k��-\frac{5��}{12}��k��-\frac{��}{12}����k��Z$ |
���� ���������жϺ����ĶԳ��ԣ�������Ǻ��������ʽ�����ʽ����ת����⼴�ɣ�
��� �⣺��f��-1+x��=f��3-x����
�ຯ������$\frac{-1+x+3-x}{2}$=1�Գ��ԣ�
��log82$\sqrt{2}$=log82${\;}^{\frac{3}{2}}$=$\frac{lo{g}_{2}{2}^{\frac{3}{2}}}{lo{g}_{2}8}$=$\frac{\frac{3}{2}}{3}$=$\frac{1}{2}$��
���ʽ$f��sin2�ȣ���f��log_8{2\sqrt{2}}��$�ȼ�Ϊf��sin2�ȣ���f��$\frac{1}{2}$����
�ߵ�x��1ʱ��f��x������������
�൱x��1ʱ��f��x�������ݼ���
��ʽ�ȼ�Ϊsin2�ȣ�$\frac{1}{2}$��
��2k��+$\frac{��}{6}$��2�ȣ�2k��+$\frac{5��}{6}$��k��Z��
��k��+$\frac{��}{12}$���ȣ�k��+$\frac{5��}{12}$��k��Z��
�ʲ���ʽ�Ľ⼯Ϊ��k��+$\frac{��}{12}$��k��+$\frac{5��}{12}$����k��Z��
��ѡ��A
���� ������Ҫ���鲻��ʽ����⣬���ݺ����Գ��Ժ͵�����֮��Ĺ�ϵ������ʽ����ת���ǽ������Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | l��m��l��ƽ��� | B�� | l��m��l��ƽ��� | C�� | l��m��l��ƽ��� | D�� | l��m��l��ƽ��� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
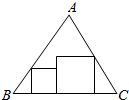 �ӵȱ�������ֽƬABC�ϣ�������ͼ��ʾ�����������Σ�����BC=3+$\sqrt{3}$���������������ε����֮�͵���СֵΪ$\frac{9}{2}$��
�ӵȱ�������ֽƬABC�ϣ�������ͼ��ʾ�����������Σ�����BC=3+$\sqrt{3}$���������������ε����֮�͵���СֵΪ$\frac{9}{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| �ɼ��ȼ� | A | B | C | D | E |
| �ɼ����֣� | 90 | 70 | 60 | 40 | 30 |
| ���������� | 4 | 6 | 10 | 7 | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ij�Ƽ��о�����һ�����з��IJ�Ʒ���Ƚ��м�⣨��λ��mm������ͼ�Ǽ������Ƶ�ʷֲ�ֱ��ͼ���ݴ˹���������Ʒ����λ��Ϊ��������
ij�Ƽ��о�����һ�����з��IJ�Ʒ���Ƚ��м�⣨��λ��mm������ͼ�Ǽ������Ƶ�ʷֲ�ֱ��ͼ���ݴ˹���������Ʒ����λ��Ϊ��������| A�� | 20 | B�� | 22.5 | C�� | 22.75 | D�� | 25 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com