
分析 ( I)由余弦定理和正弦定理求出a、sinA、sinB的值;
(II)由二倍角与两角和的正弦公式,即可求出$sin(2A+\frac{π}{3})$的值.
解答 解:( I)△ABC中,$cosA=\frac{7}{8}$,c-a=2,b=3;
∴a2=b2+c2-2bccosA=9+(2+a)2-$\frac{21}{4}$(2+a),
即9+4a+4-$\frac{21}{4}$a-$\frac{21}{2}$=0,
解得a=2;
又∵cosA=$\frac{7}{8}$,且0<A<π,
∴sinA=$\sqrt{1{-cos}^{2}A}$=$\frac{\sqrt{15}}{8}$;
由$\frac{a}{sinA}$=$\frac{b}{sinB}$,
∴$\frac{2×8}{\sqrt{15}}$=$\frac{3}{sinB}$,
解得sinB=$\frac{3\sqrt{15}}{16}$;
(II)∵sin2A=2sinAcosA
=2×$\frac{\sqrt{15}}{8}$×$\frac{7}{8}$
=$\frac{7\sqrt{15}}{32}$,
cos2A=cos2A-sin2A
=${(\frac{7}{8})}^{2}$-${(\frac{\sqrt{15}}{8})}^{2}$
=$\frac{17}{32}$,
∴$sin(2A+\frac{π}{3})$=sin2Acos$\frac{π}{3}$+cos2Asin$\frac{π}{3}$
=$\frac{7\sqrt{15}}{32}$×$\frac{1}{2}$+$\frac{17}{32}$×$\frac{\sqrt{3}}{2}$
=$\frac{7\sqrt{15}+17\sqrt{3}}{64}$.
点评 本题考查了正弦、余弦定理以及三角恒等变换的应用问题,是基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{6}$ | B. | $2\sqrt{2}$ | C. | $2\sqrt{3}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1) | B. | (-∞,3) | C. | (-2,1) | D. | (-1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
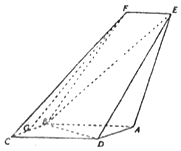 如图,四边形ABCD是平行四边形,平面AED⊥平面ABCD,EF∥AB,AB=2,BC=EF=1,AE=$\sqrt{6}$,DE=3,∠BAD=60°,G为BC的中点.
如图,四边形ABCD是平行四边形,平面AED⊥平面ABCD,EF∥AB,AB=2,BC=EF=1,AE=$\sqrt{6}$,DE=3,∠BAD=60°,G为BC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com