练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    求到定点A（2，0）的距离与直线x=4的距离之比为
    		2
    2
    的动点的轨迹方程，并说明曲线的形状．
    考点：轨迹方程
    专题：圆锥曲线的定义、性质与方程
    分析：设出动点坐标，由题意列出关系式，代入点的坐标求得动点的轨迹方程．
    解答： 解：设动点为M，坐标为（x，y），
    再设动点M到直线x=4的距离为d，
    由题意得：
    |MA|
    d
    =
    		2
    2
    ，即
    		(x-2)2+y2
    |x-4|
    =
    		2
    2
    ，
    整理得：
    x2
    8
    +
    y2
    4
    =1    ．
    ∴动点的轨迹是焦点在x轴上的椭圆．
    点评：本题考查了椭圆的定义，考查了利用求轨迹方程的方法求椭圆的方程，是中档题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

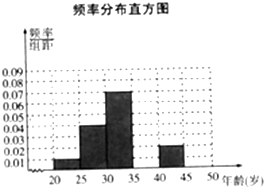    为调查市民对汽车品牌的认可度，在秋季车展上，从有意购车的500名市民中，随机抽样100名市民，按年龄情况进行统计的频率分布表Ⅰ和频率分布直方图2
    频率分布表Ⅰ
    分组（单位：岁）频数频率
    [20，25]50.05
    [25，30]200.20
    [30，35]①0.350
    [35，40]30②
    [40，45]100.10
    合计1001.000
    （1）频率分布表中的①②位置应填什么数？并补全频率分布直方图，再根据频率分布直方图统计这500名志愿者得平均年龄；
    （2）在抽出的100名志愿者中按年龄采用分层抽样的方法抽取20名参加的宣传活动，再从这20名中选取2名志愿者担任主要发言人．记这2名志愿者中“年龄低于30岁”的人数为X，求X的分布列及数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下列结论中正确的是（　　）
    A、偶函数的图象一定与y轴相交
    B、奇函数y=f（x）在x=0处有定义，则f（0）=0
    C、奇函数y=f（x）图象一定过原点
    D、图象过原点的奇函数必是单调函数

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知|
    a
    |=2，|
    b
    |=3，
    a
    ，
    b
    的夹角为60°，则|2
    a
    -
    b
    |=
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）是定义域为R的偶函数，当x≥0时，f（x）=x（2-x）．
    （1）在给定的图示中画出函数f（x）的图象（不需列表）；
    （2）求函数f（x）的解析式；
    （3）讨论方程f（x）-k=0的根的情况．（只需写出结果，不要解答过程）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    双曲线
    x2
    b2
    -
    y2
    a2
    =-1与抛物线y=
    1
    8
    x2有一个公共焦点F，双曲线上过点F且垂直实轴的弦长为
    2
    		3
    3
    ，则双曲线的离心率等于（　　）
    A、2
    B、
    2
    		3
    3
    C、
    3
    		2
    2
    D、
    		3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设集合M={x|x=
    k
    2
    +
    1
    2
    ，k∈Z}，N={x|x=
    k
    4
    +
    1
    2
    ，k∈Z}，则（　　）
    A、M=NB、M?N
    C、M?ND、M∩N=∅

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    气象意义上从春季进入夏季的标志为：“连续5天的日平均温度均不低于22℃”．现有甲、乙、丙三地连续5天的日平均温度的记录数据（记录数据都是正整数）：
    ①甲地：5个数据的中位数为24，众数为22；
    ②乙地：5个数据的中位数为27，总体均值为24；
    ③丙地：5个数据中有一个数据是32，总体均值为26，总体方差为10.8；
    则肯定进入夏季的地区有（　　）
    A、①②③B、①③C、②③D、①

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知A（x1，y1），B（x2，y2）是直线ax+by+c=0（b≠0）上两点，则|AB|等于（　　）
    A、
    |x1-x2|
    		a2+b2
    B、|
    x1-x2
    b
    |•
    		a2+b2
    C、|x1-x2|•
    		a2+b2
    D、|
    x1-x2
    a
    |•
    		a2+b2

    查看答案和解析>>

    同步练习册答案