
| A. | 3$\sqrt{3}$ | B. | 2$\sqrt{5}$ | C. | 3$\sqrt{2}$ | D. | 3 |
分析 由题意画出几何体的图形,推出四面体的外接球的球心的位置,利用球的半径建立方程,即可求出a的值.
解答 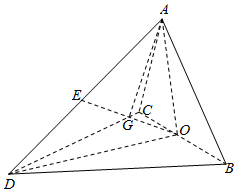 解:表面积为20π的球的半径为$\sqrt{5}$.
解:表面积为20π的球的半径为$\sqrt{5}$.
画出几何体的图形,BC=a,BC的中点为O,连接AO,DO,则AO⊥BC,DO⊥BC,
∴BC⊥平面AOD,
取AD的中点E,则OE⊥AD,球的球心在AD的中点E与O的连线上,
设球心为G,
∵OA=OD=$\sqrt{12-\frac{{a}^{2}}{4}}$,AD=2$\sqrt{3}$,
∴OE=$\sqrt{9-\frac{{a}^{2}}{4}}$
设球的半径为R,GE=x,则R2=5=3+x2=$\frac{{a}^{2}}{4}$+($\sqrt{9-\frac{{a}^{2}}{4}}$-x)2,
∴x=$\sqrt{2}$,a=3$\sqrt{2}$
故选:C..
点评 考查四面体的外接球的半径的求法,考查空间想象能力,能够判断球心的位置是本题解答的关键,考查计算能力,转化思想.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{1}{2}$) | B. | (0,$\frac{1}{2}$) | C. | (-∞,$\frac{1}{2}$] | D. | (0,$\frac{1}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ①④ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com