
分析 将四面体补成长方体,通过求解长方体的对角线就是球的直径,然后求解外接球的表面积.
解答 解:由题意可采用割补法,考虑到四面体ABCD的四个面为全等的三角形,
所以可在其每个面补上一个以2,$\sqrt{2}$,$\sqrt{2}$为三边的三角形作为底面,
且以分别x,y,z长、两两垂直的侧棱的三棱锥,
从而可得到一个长、宽、高分别为x,y,z的长方体,
并且x2+y2=4,x2+z2=2,y2+z2=2,
则有(2R)2=x2+y2+z2=4(R为球的半径),
所以球的表面积为S=4πR2=4π.
故答案为:4π.
点评 本题考查几何体的外接球的表面积的求法,割补法的应用,判断外接球的直径是长方体的对角线的长是解题的关键之一.


 优百分课时互动系列答案
优百分课时互动系列答案科目:高中数学 来源: 题型:解答题
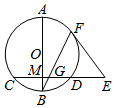 如图,AB是圆O的直径,弦CD⊥AB于点M,点E是CD延长线上一点,AB=10,CD=8,3ED=4OM,EF切圆O于F,BF交CD于点G.
如图,AB是圆O的直径,弦CD⊥AB于点M,点E是CD延长线上一点,AB=10,CD=8,3ED=4OM,EF切圆O于F,BF交CD于点G.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
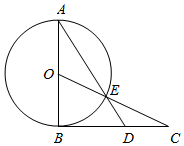 如图,AB为⊙O的直径,过点B作⊙O的切线BC,OC交⊙O于点E,AE的延长线交BC于点D.
如图,AB为⊙O的直径,过点B作⊙O的切线BC,OC交⊙O于点E,AE的延长线交BC于点D.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3$\sqrt{3}$ | B. | 2$\sqrt{5}$ | C. | 3$\sqrt{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 四面体ABCD满足:棱CD?平面α,三条棱AB,AC,AD两两垂直且相等,E为棱BC的中点,如图所示,当四而体ABCD绕CD旋转时,直线AE与平面α所成角的最大值为$\frac{π}{3}$.
四面体ABCD满足:棱CD?平面α,三条棱AB,AC,AD两两垂直且相等,E为棱BC的中点,如图所示,当四而体ABCD绕CD旋转时,直线AE与平面α所成角的最大值为$\frac{π}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com