
分析 (1)由被开方式非负,可得定义域为R,化简f(x)═|2x-1|,讨论x≥0,x<0,结合指数函数的单调性,可得f(x)的单调区间;
(2)由f(x)的单调区间,可得f(0)取得最小值;
(3)将f(x)写成分段函数,由指数函数和分段函数的图象画法,可得f(x)的图象.
解答 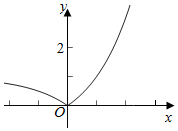 解:(1)要使f(x)有意义,可得1-2x+1+4x≥0,
解:(1)要使f(x)有意义,可得1-2x+1+4x≥0,
即为(2x-1)2≥0,
由2x>0,可得函数的定义域为R,
则f(x)=$\sqrt{({2}^{x}-1)^{2}}$=|2x-1|,
当x≥0,即2x≥1,即有f(x)=2x-1;f(x)递增;
当x<0时,即2x<1,即有f(x)=1-2x;f(x)递减.
综上可得,f(x)的增区间为[0,+∞),减区间为(-∞,0);
(2)由(1)可得,f(x)的增区间为[0,+∞),减区间为(-∞,0),
可得f(0)取得最小值|20-1|=0
(3)由f(x)=$\sqrt{({2}^{x}-1)^{2}}$=|2x-1|
=$\left\{\begin{array}{l}{{2}^{x}-1,x≥0}\\{1-{2}^{x},x<0}\end{array}\right.$,
由分段函数和指数函数的图象,可得f(x)的图象,如右:
点评 本题考查函数的性质和应用,主要是函数的单调性和最值,同时考查函数的图象,注意运用指数函数的图象和性质,考查化简整理的运算能力,属于中档题.


 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
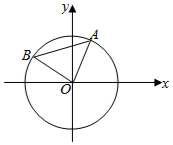 A、B是单位圆O上的动点,且A、B分别在第一、二象限.C是圆O与x轴正半轴的交点,△AOB为正三角形.记∠AOC=α.
A、B是单位圆O上的动点,且A、B分别在第一、二象限.C是圆O与x轴正半轴的交点,△AOB为正三角形.记∠AOC=α.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com