
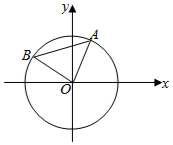
 A、B是单位圆O上的动点,且A、B分别在第一、二象限.C是圆O与x轴正半轴的交点,△AOB为正三角形.记∠AOC=α.
A、B是单位圆O上的动点,且A、B分别在第一、二象限.C是圆O与x轴正半轴的交点,△AOB为正三角形.记∠AOC=α.分析 (Ⅰ)利用任意角的三角函数的定义,三角恒等变换,求得所给式子的值.
(Ⅱ)由题意可得∠AOB=$\frac{π}{3}$,α∈(0,$\frac{π}{2}$),由余弦定理以及余弦函数的定义域和值域,求得|BC|2的取值范围.
解答 解:(Ⅰ)若A点的坐标为$(\frac{3}{5},\frac{4}{5})$,则cosα=$\frac{3}{5}$,sinα=$\frac{4}{5}$,
∴$\frac{{{{sin}^2}α+sin2a}}{{{{cos}^2}α+cos2α}}$=$\frac{{sin}^{2}α+2sinαcosα}{{3cos}^{2}α-1}$=$\frac{\frac{16}{25}+\frac{24}{25}}{3•\frac{9}{25}-1}$=20.
(Ⅱ)由题意可得∠AOB=$\frac{π}{3}$,
∴由余弦定理可得|BC|2 =OB2+OC2-2OB•OC•cos($\frac{π}{3}$+α)=1+1-2cos($\frac{π}{3}$+α),
∵∠AOC=α∈(0,$\frac{π}{2}$),∴$\frac{π}{3}$+α∈($\frac{π}{3}$,$\frac{5π}{6}$),cos($\frac{π}{3}$+α)∈(-$\frac{\sqrt{3}}{2}$,$\frac{1}{2}$),
∴-2cos($\frac{π}{3}$+α)∈(-1,$\sqrt{3}$),∴1+1-2cos($\frac{π}{3}$+α)∈(1,2+$\sqrt{3}$).
点评 本题主要考查任意角的三角函数的定义,三角恒等变换,余弦定理,余弦函数的值域,属于中档题.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\{m|m<\frac{2}{3}\}$ | B. | {0,2} | C. | $\{m|-1<m<\frac{4}{3}\}$ | D. | {0} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $±\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{5π}{6}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
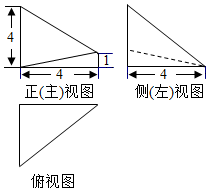 已知某几何体的三视图(如图),其中俯视图和侧(左)视图都是腰长为4的等腰直角三角形,正(主)视图为直角梯形,则此几何体的体积V的大小为( )
已知某几何体的三视图(如图),其中俯视图和侧(左)视图都是腰长为4的等腰直角三角形,正(主)视图为直角梯形,则此几何体的体积V的大小为( )| A. | $\frac{35}{3}$ | B. | 12 | C. | 16 | D. | $\frac{40}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com