
分析 (1)根据函数经过原点求出b=0,然后根据f′(x)=1,求出a的值,再根据an=Sn-Sn-1求出an的通项公式,
(2)由an+log3n=log3bn,得bn=n-32n,即可得Tn=b1+b2+b3+…+bn=1-32+2-34+3-36+…+n-32n,再写出9Tn=34+2-36+3-38+…+n-32n+2,两式相减整理可得数列{bn}的前n项和.
解答 解:(1)∵y=f(x)的图象过原点,
∴f(x)=x2-ax
由f′(x)=2x-a得f′(x)=2-a=1,
∴a=1,
∴f(x)=x2-x,
∴Sn=n2-n,an=Sn-Sn-1=n2-n-[(n-1)2-(n-1)]=2n-2,(n≥2))
∵a1=S1=0,
∴数列{an}的通项公式为an=2n-2(n∈N+).
(2)由an+log3n=log3bn,得bn=n•32n,
∴Tn=b1+b2+b3+…+bn=1•32+2•34+3•36+…+n•32n ①
∴9Tn=34+2•36+3•38+…+n•32n+2 ②,
②-①得8Tn=n-32n+2-9-(34+36+…+32n )=n-32n+2-$\frac{{3}^{2n+2}-{3}^{4}}{8}$,
∴Tn=$\frac{n-{3}^{2m+2}}{8}$-$\frac{{3}^{2n+2}-81}{64}$=$\frac{(8n-1)•{3}^{2n}+9}{64}$.
点评 本题主要考查数列的求和和等差数列的通项公式的知识点,解答本题的关键是求出a和b的值,熟练掌握等差、等比数列的求和公式.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\frac{1}{8}$ | C. | -2 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “?x∈R,x2-4x+1>0”的否定是“?x∈R,x2-4x+1<0” | |
| B. | 若x≥5,y≥6,则x+y≥11的逆否命题是假命题 | |
| C. | “x>1”是“$\frac{1}{x}<1$”的充要条件 | |
| D. | 已知α,β为两个不同的平面,m为α内的一条直线,则“α⊥β”是“m⊥β”的必要不充分条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
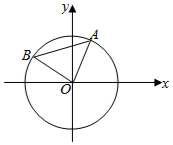 A、B是单位圆O上的动点,且A、B分别在第一、二象限.C是圆O与x轴正半轴的交点,△AOB为正三角形.记∠AOC=α.
A、B是单位圆O上的动点,且A、B分别在第一、二象限.C是圆O与x轴正半轴的交点,△AOB为正三角形.记∠AOC=α.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份中的x | 0 | 1 | 2 | 3 | 4 |
| 人口总数y | 5 | 7 | 8 | 11 | 19 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com