
| A. | “?x∈R,x2-4x+1>0”的否定是“?x∈R,x2-4x+1<0” | |
| B. | 若x≥5,y≥6,则x+y≥11的逆否命题是假命题 | |
| C. | “x>1”是“$\frac{1}{x}<1$”的充要条件 | |
| D. | 已知α,β为两个不同的平面,m为α内的一条直线,则“α⊥β”是“m⊥β”的必要不充分条件 |
分析 A.根据特称命题的否定是全称命题进行判断
B.根据逆否命题的等价性判断原命题为真命题即可,
C.根据不等式的性质以及充分条件和必要条件的定义进行判断,
D.根据线面垂直和面面垂直的判定定理以及充分条件和必要条件的定义进行判断.
解答 解:A.“?x∈R,x2-4x+1>0”的否定是“?x∈R,x2-4x+1≤0”,故A错误,
B.若x≥5,y≥6,则x+y≥11,则原命题为真命题,则逆否命题也为真命题,故B错误,
C.由$\frac{1}{x}<1$得x>1或x<0,则“x>1”是“$\frac{1}{x}<1$”的充分不必要条件,故C错误,
D.由平面与平面垂直的判定定理知如果m为平面α内的一条直线,且m⊥β,则α⊥β,反之,α⊥β时,若m平行于α和β的交线,则m∥β,所以不一定能得到m⊥β,所以“α⊥β”是“m⊥β”的必要不充分条件.故D正确
故选:D
点评 本题主要考查命题的真假判断,涉及含有量词的命题的否定,充分条件和必要条件的判断以及四种命题真假的关系,涉及的知识点较多,综合性较强,但难度不大.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{2π}{5}$ | B. | $\frac{3π}{5}$ | C. | $\frac{4π}{5}$ | D. | π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | b<a<c | B. | b<c<a | C. | a<b<c | D. | c<b<a |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | (1,-3) | C. | (-1,3) | D. | (-1,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
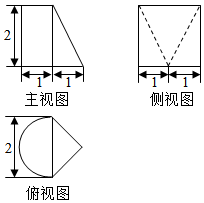
| A. | $\frac{2π}{3}+4$ | B. | $\frac{2π+4}{3}$ | C. | $\frac{π}{3}+4$ | D. | $π+\frac{4}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com