Question

12．如图为某几何体的三视图，则其体积为（　　）

• A． $\frac{2π}{3}+4$
• B． $\frac{2π+4}{3}$
• C． $\frac{π}{3}+4$
• D． $π+\frac{4}{3}$

Answer 1

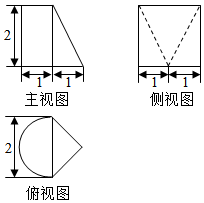
分析 由三视图可知：该几何体由左右两部分组成，左面是一个圆柱的一半，右面是多面体（可以看做是由一个三棱柱去掉一个三棱锥后剩下的几何体）．

解答 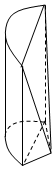解：由三视图可知：该几何体由左右两部分组成，左面是一个圆柱的一半，
右面是多面体（可以看做是由一个三棱柱去掉一个三棱锥后剩下的几何体）．
该几何体的体积=$π×{1}^{2}×\frac{1}{2}×2$+$（\frac{1}{2}×2×1×2-\frac{1}{3}×\frac{1}{2}×2×1×2）$=$π+\frac{4}{3}$．
故选：D．

点评 本题考查了三视图的有关计算、柱体与锥体的体积计算公式，考查了推理能力与计算能力，属于中档题．