
分析 利用错位相减法计算可知Sn=4-$\frac{n+2}{{2}^{n-1}}$,化简可知4-$\frac{1}{{2}^{n-2}}$≥2,从而问题转化为解不等式|λ+1|<2,计算即得结论.
解答 解:∵Sn是数列{$\frac{n}{{2}^{n-1}}$}的前n项和,
∴Sn=1•$\frac{1}{{2}^{0}}$+2•$\frac{1}{2}$+3•$\frac{1}{{2}^{2}}$+…+n•$\frac{1}{{2}^{n-1}}$,
$\frac{1}{2}$Sn=1•$\frac{1}{2}$+2•$\frac{1}{{2}^{2}}$+…+(n-1)•$\frac{1}{{2}^{n-1}}$+n•$\frac{1}{{2}^{n}}$,
两式相减,得:$\frac{1}{2}$Sn=1+$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n-1}}$-n•$\frac{1}{{2}^{n}}$=$\frac{1-\frac{1}{{2}^{n}}}{1-\frac{1}{2}}$-n•$\frac{1}{{2}^{n}}$=2-$\frac{n+2}{{2}^{n}}$,
即Sn=4-$\frac{n+2}{{2}^{n-1}}$,
∴Sn+$\frac{n}{{2}^{n-1}}$=4-$\frac{n+2}{{2}^{n-1}}$+$\frac{n}{{2}^{n-1}}$=4-$\frac{1}{{2}^{n-2}}$,
∵$\frac{1}{{2}^{n-2}}$随着n的增大而减小,
∴当n=1时4-$\frac{1}{{2}^{n-2}}$取最小值4-$\frac{1}{{2}^{1-2}}$=2,
∴|λ+1|<2,解得:-3<λ<1,
故答案为:-3<λ<1.
点评 本题是一道关于数列与不等式的综合题,考查错位相减法,考查数列的单调性,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | (1,-3) | C. | (-1,3) | D. | (-1,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
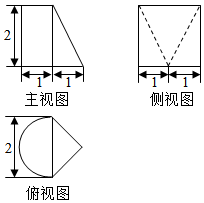
| A. | $\frac{2π}{3}+4$ | B. | $\frac{2π+4}{3}$ | C. | $\frac{π}{3}+4$ | D. | $π+\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
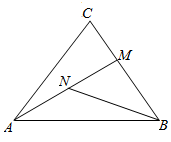 如图,在边长为1的正三角形ABC中,$\overrightarrow{BM}$=2$\overrightarrow{MC}$,N为AM的中点.
如图,在边长为1的正三角形ABC中,$\overrightarrow{BM}$=2$\overrightarrow{MC}$,N为AM的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 2015年12月,京津冀等地数城市指数“爆表”,北方此轮污染为2015年以来最严重的污染过程.为了探究车流量与PM2.5的浓度是否相关,现采集到北方某城市2015年12月份星期一到星期日某一时间段车流量与PM2.5的数据如表:
2015年12月,京津冀等地数城市指数“爆表”,北方此轮污染为2015年以来最严重的污染过程.为了探究车流量与PM2.5的浓度是否相关,现采集到北方某城市2015年12月份星期一到星期日某一时间段车流量与PM2.5的数据如表:| 时间 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 |
| 车流量x(万辆) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| PM2.5的浓度y(微克/立方米) | 27 | 31 | 35 | 41 | 49 | 56 | 62 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com