
 2015年12月,京津冀等地数城市指数“爆表”,北方此轮污染为2015年以来最严重的污染过程.为了探究车流量与PM2.5的浓度是否相关,现采集到北方某城市2015年12月份星期一到星期日某一时间段车流量与PM2.5的数据如表:
2015年12月,京津冀等地数城市指数“爆表”,北方此轮污染为2015年以来最严重的污染过程.为了探究车流量与PM2.5的浓度是否相关,现采集到北方某城市2015年12月份星期一到星期日某一时间段车流量与PM2.5的数据如表:| 时间 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 |
| 车流量x(万辆) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| PM2.5的浓度y(微克/立方米) | 27 | 31 | 35 | 41 | 49 | 56 | 62 |
分析 (1)利用描点法可得数据的散点图;
(2)根据公式求出b,a,可写出线性回归方程;
(3)(i)根据(2)的性回归方程,代入x=8求出PM2.5的浓度,(ii)由$\frac{169}{28}$x+$\frac{132}{7}$≤100,解得x的取值范围.
解答 解:画出车流量和PM2.5浓度的散点图;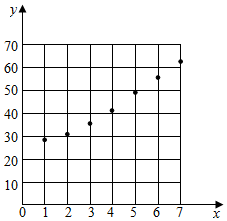
(2)由数据可得:$\overline{x}$=$\frac{1}{7}$(1+2+3+4+5+6+7)=4,
$\overline{y}$=$\frac{1}{7}$(27+31+35+41+49+56+62)=43,
$\sum_{i=1}^{7}$xiyi=1373,$\sum_{i=1}^{7}$${x}_{i}^{2}$=140,
$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$=$\frac{1373-1204}{140-112}$=$\frac{169}{28}$,
$\stackrel{^}{a}$=$\overline{y}$-b$\overline{x}$=$\frac{132}{7}$,
故y关于x的线性回归方程为$\stackrel{^}{y}$=$\frac{169}{28}$x+$\frac{132}{7}$,
(3)(i)当车流量为8万辆时,即x=8时,$\stackrel{^}{y}$=$\frac{169}{28}$×8+$\frac{132}{7}$=$\frac{470}{7}$,
故车流量为8万辆时,PM2.5的浓度$\frac{470}{7}$,
(ii)根据题意信息$\frac{169}{28}$x+$\frac{132}{7}$≤100,
即当x≤13.44时,
所要使该市某日空气质量为优活为良,则应控制当天车流量在13万辆以内.
点评 本题主要考查了线性回归分析的方法,包括散点图,用最小二乘法求参数,以及用回归方程进行预测等知识,考查了考生数据处理和运算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
 如图,在侧棱和底面垂直的三棱柱ABC-A1B1C1中,AB=1,AC=$\sqrt{3}$,BC=2,AA1=$\sqrt{6}$,点P为CC1的中点.
如图,在侧棱和底面垂直的三棱柱ABC-A1B1C1中,AB=1,AC=$\sqrt{3}$,BC=2,AA1=$\sqrt{6}$,点P为CC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{{2\sqrt{x}}}$ | B. | -$\frac{1}{{2\sqrt{x}}}$ | C. | -$\frac{{\sqrt{x}}}{2}$ | D. | $\frac{{\sqrt{x}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
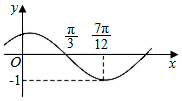 函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,0<φ<$\frac{π}{2}$)的图象如图所示.
函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,0<φ<$\frac{π}{2}$)的图象如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com