
 如图,在侧棱和底面垂直的三棱柱ABC-A1B1C1中,AB=1,AC=$\sqrt{3}$,BC=2,AA1=$\sqrt{6}$,点P为CC1的中点.
如图,在侧棱和底面垂直的三棱柱ABC-A1B1C1中,AB=1,AC=$\sqrt{3}$,BC=2,AA1=$\sqrt{6}$,点P为CC1的中点.分析 (1)推导出AA1⊥AB,AB⊥AC,从而AB⊥A1C,再推导出A1C⊥AP,由此能证明A1C⊥平面ABP.
(2)以A为坐标原点,以AB为x轴,AC为y轴,AA1为z轴,建立空间直角坐标系,利用向量法能求出平面ABP与平面A1B1P所成二面角的正弦值.
解答 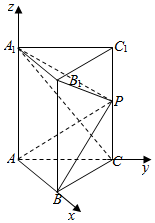 证明:(1)在侧棱和底面垂直的三棱柱ABC-A1B1C1中,AA1⊥平面ABC,
证明:(1)在侧棱和底面垂直的三棱柱ABC-A1B1C1中,AA1⊥平面ABC,
∵AB?平面ABC,∴AA1⊥AB,
∵AB=1,AC=$\sqrt{3}$,BC=2,AA1=$\sqrt{6}$,点P为CC1的中点,∴BC2=AB2+AC2,∴AB⊥AC,
又AA1∩AC=A,∴AB⊥A1C,
在矩形ACC1A1中,A1C=$\sqrt{A{C}^{2}+A{{A}_{1}}^{2}}$=3,AP=$\sqrt{A{C}^{2}+C{P}^{2}}$=$\frac{3\sqrt{2}}{2}$,
在Rt△A1CA中,sin∠A1CA=$\frac{A{A}_{1}}{{A}_{1}C}$=$\frac{\sqrt{6}}{3}$,
在Rt△PAC中,cos$∠PAC=\frac{AC}{AP}$=$\frac{\sqrt{6}}{3}$,
∴sin∠A1CA=cos∠PAC,∴∠PAC+∠A1CA=90°,
∴A1C⊥AP,
∵AP∩AB=A,∴A1C⊥平面ABP.
解:(2)由(1)知AB⊥AC,AA1⊥AB,AA1⊥AC,
以A为坐标原点,以AB为x轴,AC为y轴,AA1为z轴,建立空间直角坐标系,
则A(0,0,0),B(1,0,0),A1(0,0,$\sqrt{6}$),C(0,$\sqrt{3}$,0),P(0,$\sqrt{3}$,$\frac{\sqrt{6}}{2}$),
$\overrightarrow{{A}_{1}{B}_{1}}=\overrightarrow{AB}$=(1,0,0),$\overrightarrow{{A}_{1}P}=(0,\sqrt{3},-\frac{\sqrt{6}}{2})$,
设平面A1B1P的法向量为$\overrightarrow{m}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{{A}_{1}{B}_{1}}=x=0}\\{\overrightarrow{m}•\overrightarrow{{A}_{1}P}=\sqrt{3}y-\frac{\sqrt{6}}{2}z=0}\end{array}\right.$,
令y=1,得$\overrightarrow{m}$=(0,1,$\sqrt{2}$),
由(1)知平面ABP的一个法向量为$\overrightarrow{C{A}_{1}}$=(0,-$\sqrt{3}$,$\sqrt{6}$),
∴cos<$\overrightarrow{m},\overrightarrow{C{A}_{1}}$>=$\frac{\overrightarrow{m}•\overrightarrow{C{A}_{1}}}{|\overrightarrow{m}|•|\overrightarrow{C{A}_{1}}|}$=$\frac{-\sqrt{3}+2\sqrt{3}}{\sqrt{3}×\sqrt{3+6}}$=$\frac{1}{3}$,
∴sin<$\overrightarrow{m}•\overrightarrow{C{A}_{1}}$>=$\sqrt{1-(\frac{1}{3})^{2}}$=$\frac{2\sqrt{2}}{3}$.
即平面ABP与平面A1B1P所成二面角的正弦值为$\frac{2\sqrt{2}}{3}$.
点评 本题考查线面垂直的证明,考查二面角的正弦值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.


 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:高中数学 来源: 题型:选择题
| A. | b<a<c | B. | b<c<a | C. | a<b<c | D. | c<b<a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | (1,-3) | C. | (-1,3) | D. | (-1,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某中学高三(10)班女同学有45名,男同学有15名,老师按照分层抽样的方法组建了一个4人的课外兴趣小组.
某中学高三(10)班女同学有45名,男同学有15名,老师按照分层抽样的方法组建了一个4人的课外兴趣小组.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
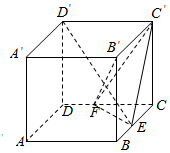 如图,在棱长为2的正方体ABCD-A′B′C′D′中,点E,F分别是棱BC,CD上的动点.
如图,在棱长为2的正方体ABCD-A′B′C′D′中,点E,F分别是棱BC,CD上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
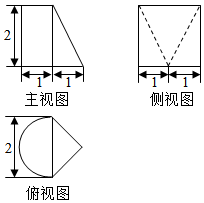
| A. | $\frac{2π}{3}+4$ | B. | $\frac{2π+4}{3}$ | C. | $\frac{π}{3}+4$ | D. | $π+\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 2015年12月,京津冀等地数城市指数“爆表”,北方此轮污染为2015年以来最严重的污染过程.为了探究车流量与PM2.5的浓度是否相关,现采集到北方某城市2015年12月份星期一到星期日某一时间段车流量与PM2.5的数据如表:
2015年12月,京津冀等地数城市指数“爆表”,北方此轮污染为2015年以来最严重的污染过程.为了探究车流量与PM2.5的浓度是否相关,现采集到北方某城市2015年12月份星期一到星期日某一时间段车流量与PM2.5的数据如表:| 时间 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 |
| 车流量x(万辆) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| PM2.5的浓度y(微克/立方米) | 27 | 31 | 35 | 41 | 49 | 56 | 62 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com