
科目:高中数学 来源: 题型:解答题
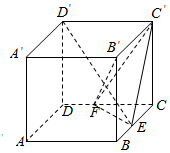 如图,在棱长为2的正方体ABCD-A′B′C′D′中,点E,F分别是棱BC,CD上的动点.
如图,在棱长为2的正方体ABCD-A′B′C′D′中,点E,F分别是棱BC,CD上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 2015年12月,京津冀等地数城市指数“爆表”,北方此轮污染为2015年以来最严重的污染过程.为了探究车流量与PM2.5的浓度是否相关,现采集到北方某城市2015年12月份星期一到星期日某一时间段车流量与PM2.5的数据如表:
2015年12月,京津冀等地数城市指数“爆表”,北方此轮污染为2015年以来最严重的污染过程.为了探究车流量与PM2.5的浓度是否相关,现采集到北方某城市2015年12月份星期一到星期日某一时间段车流量与PM2.5的数据如表:| 时间 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 |
| 车流量x(万辆) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| PM2.5的浓度y(微克/立方米) | 27 | 31 | 35 | 41 | 49 | 56 | 62 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
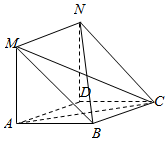 如图,在菱形ABCD中,MA⊥平面ABCD,且四边形ADNM是平行四边形.已知MA=3,AD=4,∠BAD=60°.
如图,在菱形ABCD中,MA⊥平面ABCD,且四边形ADNM是平行四边形.已知MA=3,AD=4,∠BAD=60°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com