
| 年份中的x | 0 | 1 | 2 | 3 | 4 |
| 人口总数y | 5 | 7 | 8 | 11 | 19 |
分析 (1)根据表格画出散点图:可得y与x是正相关.
(2)根据所给的数据求出$\overline{x}$,$\overline{y}$,可依据公式求得b和a的值,从而求得回归方程.
(3)在回归直线的方程中,令x=5,求得对应的y值,可得结论.
解答 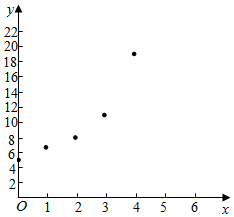 解:(1)根据表格画出散点图:可得y与x是正相关.
解:(1)根据表格画出散点图:可得y与x是正相关.
概据题中数表画出数据的散点图如下图所示.
(2)由题中数表,知:$\overline{x}$=$\frac{1}{5}$(0+1+2+3+4)=2,$\overline{y}$=$\frac{1}{5}$(5+7+8+11+19)=10,
∴b=$\frac{\sum_{i=1}^{5}{{x}_{i}x}_{i}-5\overline{x}\overline{y}}{\sum_{i=1}^{5}{{x}_{i}}^{2}-{5\overline{x}}^{2}}$=3.2,a=$\overline{y}$-b$\overline{x}$=3.6,∴回归方程为y=3.2x+3.6.
(3)当x=5时,求得y=19.6(十万)=196(万).
答:估计2019年该城市人口总数约为196万.
点评 本题主要考查两个变量的相关关系,线性回归问题,求回归直线的方程以及回归方程的应用,属于基础题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
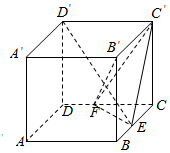 如图,在棱长为2的正方体ABCD-A′B′C′D′中,点E,F分别是棱BC,CD上的动点.
如图,在棱长为2的正方体ABCD-A′B′C′D′中,点E,F分别是棱BC,CD上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
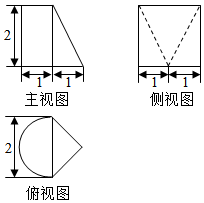
| A. | $\frac{2π}{3}+4$ | B. | $\frac{2π+4}{3}$ | C. | $\frac{π}{3}+4$ | D. | $π+\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
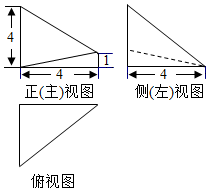 已知某几何体的三视图(如图),其中俯视图和侧(左)视图都是腰长为4的等腰直角三角形,正(主)视图为直角梯形,则此几何体的体积V的大小为( )
已知某几何体的三视图(如图),其中俯视图和侧(左)视图都是腰长为4的等腰直角三角形,正(主)视图为直角梯形,则此几何体的体积V的大小为( )| A. | $\frac{35}{3}$ | B. | 12 | C. | 16 | D. | $\frac{40}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com