
| A. | $\{m|m<\frac{2}{3}\}$ | B. | {0,2} | C. | $\{m|-1<m<\frac{4}{3}\}$ | D. | {0} |
分析 根据周期性和奇偶性的性质进行转化求解即可.
解答 解:∵f(x)是定义在R上的奇函数,若f(x)的最小正周期为4,
∴f(3)=f(3-4)=f(-1)=-f(1)<-1,
即$f(3)=\frac{2m-5}{m+1}$<-1,即$\frac{2m-5}{m+1}$+1=$\frac{3m-4}{m+1}$<0,得-1<m<$\frac{4}{3}$,
∵f(x+4)=f(x),∴f(-2+4)=f(-2),
即f(2)=-f(2),则f(2)=0,
则f(2)=m2-2m=0,则m=0或m=2,
综上m=0,
故实数m的取值集合是{0},
故选:D.
点评 本题主要考查函数奇偶性和周期性的应用,根据周期性和奇偶性的性质进行转化是解决本题的关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6cm2 | B. | 7cm2 | C. | 9cm2 | D. | 10cm2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\frac{1}{8}$ | C. | -2 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
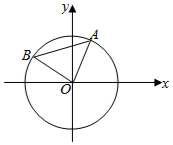 A、B是单位圆O上的动点,且A、B分别在第一、二象限.C是圆O与x轴正半轴的交点,△AOB为正三角形.记∠AOC=α.
A、B是单位圆O上的动点,且A、B分别在第一、二象限.C是圆O与x轴正半轴的交点,△AOB为正三角形.记∠AOC=α.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,4) | B. | (-4,0) | C. | (0,4) | D. | (4,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com