
分析 (Ⅰ)当a=0时,对f(x)求导,判断单调性求极值;
(Ⅱ)当-3<a<-2时,使不等式恒成立即求f(x)的最值,转化为f(λ1)-f(λ2)|max<(m+ln3)a-2ln3,然后求m 范围.
解答 解:(Ⅰ)依题意,${h^'}(x)=\frac{1}{x}+2ax$,所以$f(x)=(2-a)lnx+\frac{1}{x}+2ax$,其定义域为(0,+∞)
当a=0时,$f(x)=2lnx+\frac{1}{x}$,${f^'}(x)=\frac{2}{x}-\frac{1}{x^2}=\frac{2x-1}{x^2}$
令f′(x)=0,解得:$x=\frac{1}{2}$,当$0<x<\frac{1}{2}$时,f′(x)<0,当$x>\frac{1}{2}$时,f′(x)>0
所以当 $x=\frac{1}{2}$时,f(x)有极小值$f(\frac{1}{2})=2-ln2$,无极大值.
(Ⅱ) ${f^'}(x)=\frac{2-a}{x}-\frac{1}{x^2}+2a=\frac{{2a{x^2}+(2-a)x-1}}{x^2}=\frac{{a(2x-1)(x+\frac{1}{a})}}{x^2}$,x>0
当-3<a<-2时,$\frac{1}{3}<-\frac{1}{a}<\frac{1}{2}$,故当x∈[1,3]时,f′(x)<0,所以f(x)在[1,3]
单调递减,此时 f(x)max=f(1)=2a+1,$f{(x)_{min}}=f(3)=(2-a)ln3+\frac{1}{3}+6a$
$|f({λ_1})-f({λ_2}){|_{max}}=f(1)-f(3)=(1+2a)-[(2-a)ln3-2ln3+\frac{1}{3}+6a]$=$\frac{2}{3}-4a+(a-2)ln3$
依题意,只需(m+ln3)a-2ln3>$\frac{2}{3}-4a+(a-2)ln3$
即:$ma>\frac{2}{3}-4a$$⇒m<\frac{2}{3a}-4$
而当-3<a<-2,$⇒-\frac{13}{3}<\frac{2}{3a}-4<-\frac{38}{9}$
$⇒m<-\frac{13}{3}$.
点评 本题考查了利用导数求函数的极值以及恒成立问题求参数范围;属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | (0,3] | B. | [-1,8] | C. | (0,6] | D. | [2,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
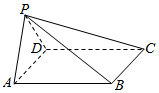 如图,已知四棱锥P-ABCD的底面为矩形,平面PAD⊥平面ABCD,$AD=2\sqrt{2}$,PA=PD=AB=2,则四棱锥P-ABCD的外接球的表面积为( )
如图,已知四棱锥P-ABCD的底面为矩形,平面PAD⊥平面ABCD,$AD=2\sqrt{2}$,PA=PD=AB=2,则四棱锥P-ABCD的外接球的表面积为( )| A. | 2π | B. | 4π | C. | 8π | D. | 12π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
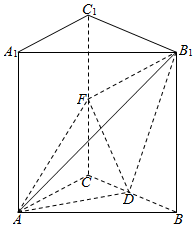 在三棱柱ABC-A1B1C1中,已知侧棱AA1⊥底面ABC,且AB=AC=5,BC=6,AA1=9,D为BC的中点,F为C1C上的动点.
在三棱柱ABC-A1B1C1中,已知侧棱AA1⊥底面ABC,且AB=AC=5,BC=6,AA1=9,D为BC的中点,F为C1C上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{1}{2}$) | B. | (0,$\frac{1}{2}$) | C. | (-∞,$\frac{1}{2}$] | D. | (0,$\frac{1}{2}$] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com