
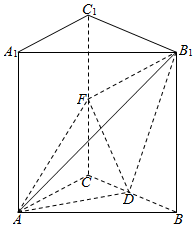
 在三棱柱ABC-A1B1C1中,已知侧棱AA1⊥底面ABC,且AB=AC=5,BC=6,AA1=9,D为BC的中点,F为C1C上的动点.
在三棱柱ABC-A1B1C1中,已知侧棱AA1⊥底面ABC,且AB=AC=5,BC=6,AA1=9,D为BC的中点,F为C1C上的动点.分析 (1)证明直线与平面垂直,关键要找到两条相交直线与之都垂直,通过证明AD⊥平面BCC1B1得AD⊥B1F,然后在矩形BCC1B1中通过证明Rt△DCF≌Rt△FC1B1得B1F⊥FD,问题从而得证.
(2)利用等体积法,将要求的三棱锥B1-ADF的体积转化为高和底面都已知的三棱锥A-B1DF的体积来求.
解答 (1)证明:∵AB=AC,D为BC中点,∴AD⊥BC,
又直三棱柱中:BB1⊥底面ABC,AD?底面ABC,
∴AD⊥BB1,
∴AD⊥平面BCC1B1,
∵B1F?平面BCC1B1
∴AD⊥B1F.
在矩形BCC1B1中:C1F=CD=3,CF=C1B1=6
∴Rt△DCF≌Rt△FC1B1,
∴∠CFD=∠C1B1F
∴∠B1FD=90°,即B1F⊥FD,
∵AD∩FD=D,
∴B1F⊥平面AFD;
(2)解:∵FD⊥B1D,BC=6,AA1=9,D为BC的中点,
∴CF=1,C1F=8,
∴${S}_{△{B}_{1}DF}$=6×9-$\frac{1}{2}×1×3$-$\frac{1}{2}×3×9$-$\frac{1}{2}×6×8$=15,
∵D为BC的中点,AB=AC=5,BC=6,
∴AD=4,
∵AD⊥平面BCC1B1,
∴三棱锥B1-ADF的体积=三棱锥A-B1DF的体积=$\frac{1}{3}×15×4$=20.
点评 本小题主要考查空间线面关系、几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力,是个中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
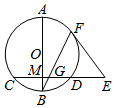 如图,AB是圆O的直径,弦CD⊥AB于点M,点E是CD延长线上一点,AB=10,CD=8,3ED=4OM,EF切圆O于F,BF交CD于点G.
如图,AB是圆O的直径,弦CD⊥AB于点M,点E是CD延长线上一点,AB=10,CD=8,3ED=4OM,EF切圆O于F,BF交CD于点G.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
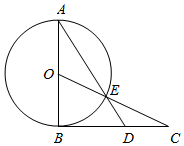 如图,AB为⊙O的直径,过点B作⊙O的切线BC,OC交⊙O于点E,AE的延长线交BC于点D.
如图,AB为⊙O的直径,过点B作⊙O的切线BC,OC交⊙O于点E,AE的延长线交BC于点D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com