
分析 (1)由题意,设人数是x人,物价为y元,则x应满足条件8x-3=7x+4.因此,可以让x从1开始检验,若条件不成立,则x递增1,一直到x满足条件为止,由此可得程序.
(2)由题意,设人数为x,鸡价为y元,则x应满足条件9x-11=6x+16.因此,可以让x从1开始检验,若条件不成立,则x递增1,一直到x满足条件为止,由此可得程序.
解答 解:翻译为现代语言,即:
(1)一些人共同买东西,每人出八元钱,则多三元钱,每人出七元钱,则少四元钱.问有多少钱,物价又是多少?
设人数是x人,物价为y元,则$\left\{\begin{array}{l}{8x-3=y}\\{7x+4=y}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=7}\\{y=53}\end{array}\right.$故共有七人,物价为五十三元.
相应的程序为:
i=1;
while i<=1 000
while 8*i-3<>7*i+4
i=i+1;
end
y=8*i-3;
print(% io (2),i,“people:”,y,“price:”);
end
(2)类似于(1)的研究,设人数为x,鸡价为y元,则$\left\{\begin{array}{l}{9x-11=y}\\{6x+16=y}\end{array}\right.$
解得$\left\{\begin{array}{l}{x=9}\\{y=70}\end{array}\right.$故共有9人,鸡价为70元.
相应的程序为:
i=1,n=1 000;
while i<=n
while 9*i-11<>6*i+16
i=i+1;
end
y=9*i-11;
print(% io(2),i,“people:”,y,“price:”);
end
点评 本题考查设计程序解决实际问题,考查学生操作能力,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 必要但不充分条件 | B. | 充分但不必要条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 336 | B. | 355 | C. | 1676 | D. | 2015 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
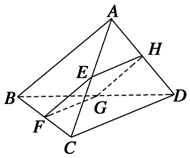 如图所示,四边形EFGH为空间四边形ABCD的一个截面,若截面为平行四边形.
如图所示,四边形EFGH为空间四边形ABCD的一个截面,若截面为平行四边形.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,2x>x2 | B. | 若a>b,c>d,则 a-c>b-d | ||
| C. | ?x∈R,ex<0 | D. | ac2<bc2是a<b的充分不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com