
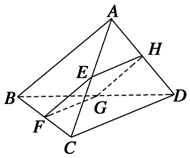
 如图所示,四边形EFGH为空间四边形ABCD的一个截面,若截面为平行四边形.
如图所示,四边形EFGH为空间四边形ABCD的一个截面,若截面为平行四边形.分析 (1)四边形EFGH为平行四边形,所以EF∥HG,HG?平面ABD,EF∥平面ABD,可得AB∥平面EFGH,同理可证,CD∥平面EFGH.
(2)构造函数的思想,设EF=x(0<x<4),由于四边形EFGH为平行四边形,∴$\frac{CF}{CB}=\frac{x}{4}$.则$\frac{FG}{6}=\frac{BF}{BC}$=$\frac{BC-CF}{BC}$=1-$\frac{x}{4}$,从而FG=6-$\frac{3x}{2}$,可得四边形EFGH的周长l=2(x+6-$\frac{3x}{2}$),由x的范围可求解.
解答 解:(1)∵四边形EFGH为平行四边形,
∴EF∥HG.
∵HG?平面ABD,∴EF∥平面ABD.
∵EF?平面ABC,平面ABD∩平面ABC=AB,AB?平面EFGH.
∴EF∥AB.∴AB∥平面EFGH.
同理可证,CD∥平面EFGH.
(2)设EF=x(0<x<4),由于四边形EFGH为平行四边形,∴$\frac{CF}{CB}=\frac{x}{4}$.
则$\frac{FG}{6}=\frac{BF}{BC}$=$\frac{BC-CF}{BC}$=1-$\frac{x}{4}$,
从而FG=6-$\frac{3x}{2}$,
∴四边形EFGH的周长l=2(x+6-$\frac{3x}{2}$)=12-x.
又∵0<x<4,则有:8<l<12,
∴四边形EFGH周长的取值范围是(8,12).
点评 本题考查了直线与平面平行的证明和构造函数思想求解周长问题.利用平行四边形的对边平行相等建立关系.属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1) | B. | (-∞,1] | C. | [1,+∞) | D. | (1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ¬p:?x∈(0,+∞),sinx≥x | B. | ¬p:?x0∈(0,+∞),sinx0≥x0 | ||
| C. | ¬p:?x∈(-∞,0],sinx≥x | D. | ¬p:?x0∈(-∞,0],sinx0≥x0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com