
分析 (Ⅰ)椭圆的方程可知:a=2,由e=$\frac{c}{a}$=$\frac{1}{2}$,求得c=1,即可求得b2=a2-c2=3,即可求得椭圆C的标准方程;
(Ⅱ)将直线方程代入椭圆方程,由韦达定理求得y1+y2=-$\frac{6mt}{3{m}^{2}+4}$,y1•y2=$\frac{3({t}^{2}-4)}{3{m}^{2}+4}$,由AB⊥AC.$\overrightarrow{AB}$•$\overrightarrow{AC}$=0,根据向量数量积的坐标表示,(x1+2)(x2+2)+y1•y2=0,即可求得t的值;
(Ⅲ)由(Ⅱ)知直线l恒过定点M(-$\frac{2}{7}$,0),AD⊥l,AD⊥DM,因此可知D的轨迹是以AM为直径的圆(除点A外),即可求得D的轨迹方程为(x+$\frac{8}{7}$)2+y2=$\frac{36}{49}$(x≠-2).
解答 解:(Ⅰ)设椭圆C的半焦距为c,a=2,
由题意知e=$\frac{c}{a}$=$\frac{1}{2}$,
∴c=1,
由b2=a2-c2=3,
椭圆C的标准方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$;…(3分)
(Ⅱ)证明:由(Ⅰ)知a=2,A(-2,0),设B(x1,y1),C(x2,y2),
把x=my+t(t≠-a),代入$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$得:(3m2+4)y2+6mty+3(t2-4)=0,…(4分)
△=36m2t2-12(3m2+4)×(t2-4)=48(3m3+4-t2)>0,
∴y1+y2=-$\frac{6mt}{3{m}^{2}+4}$,y1•y2=$\frac{3({t}^{2}-4)}{3{m}^{2}+4}$…(5分)
若AB⊥AC,
$\overrightarrow{AB}$•$\overrightarrow{AC}$=0,
则(x1+2)(x2+2)+y1•y2=(my1+t+2)(my2+t+2)+y1•y2,
=(m2+1)y1•y2+m(t+2)(y1+y2)+(t+2)2,
=(m2+1)•$\frac{3({t}^{2}-4)}{3{m}^{2}+4}$+m(t+2)(-$\frac{6mt}{3{m}^{2}+4}$)+(t+2)2,
=$\frac{(t+2)(7t+2)}{3{m}^{2}+4}$=0…(8分)
∵Q≠-2,
t=-$\frac{2}{7}$,
∴直线l:x=my+$\frac{2}{7}$,即直线l恒过定点M(-$\frac{2}{7}$,0).…(9分)
(Ⅲ)设D(x,y),由(Ⅱ)知直线l恒过定点M(-$\frac{2}{7}$,0),
∵AD⊥l,
AD⊥DM,
∴D的轨迹是以AM为直径的圆(除点A外),
则D的轨迹方程为(x+$\frac{8}{7}$)2+y2=$\frac{36}{49}$(x≠-2).…(12分)
点评 本题考查椭圆的标准方程,直线与椭圆的位置关系,考查曲线的轨迹方程,考查转化思想,属于中档题.


 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 必要但不充分条件 | B. | 充分但不必要条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
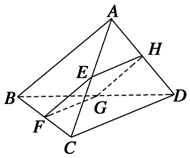 如图所示,四边形EFGH为空间四边形ABCD的一个截面,若截面为平行四边形.
如图所示,四边形EFGH为空间四边形ABCD的一个截面,若截面为平行四边形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com