
| A. | (-∞,1) | B. | (-∞,1] | C. | [1,+∞) | D. | (1,+∞) |
分析 先判断集合A,B中元素表示的几何意义,可得集合A={(x,y)|y=a}表示直线y=a,集合B={(x,y)|y=bx+1,b>0,b≠1|},表示函数y=bx+1的图象,因为A∩B=∅,所以直线y=a与曲线y=bx+1的图象无交点,据此得到a的取值范围,再根据命题的否定即可求出m的范围.
解答 解:集合A={(x,y)|y=a}表示直线y=a的图象上的所有的点,
集合B={(x,y)|y=bx+1,b>0,b≠1|},表示函数y=bx+1的图象上的所有的点,
∵A∩B=∅,∴直线y=a与曲线y=bx+1的图象无交点,
∵曲线y=bx+1的图象在直线y=1上方,
∴a≤1
∴集合A∩B≠∅,则实数a的取值范围是(1,+∞)
故选:D
点评 本题借助集合的关系判断直线与曲线y=bx+1的位置关系,并根据位置关系求参数的范围,属于综合题.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 44 | B. | 54 | C. | 88 | D. | 108 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 336 | B. | 355 | C. | 1676 | D. | 2015 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | i+2 | B. | i-2 | C. | -2-i | D. | 2-i |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
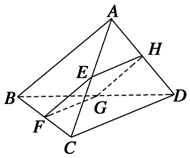 如图所示,四边形EFGH为空间四边形ABCD的一个截面,若截面为平行四边形.
如图所示,四边形EFGH为空间四边形ABCD的一个截面,若截面为平行四边形.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2013 | B. | 2014 | C. | 2015 | D. | -2014 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com