
分析 由已知求出cosα值.
(1)直接展开倍角公式及同角三角函数的基本关系式,代值后得答案;
(2)展开两角和的正弦、余弦和正切公式,代值得答案.
解答 解:∵sinα=$\frac{2}{3}$,α∈(0,$\frac{π}{2}$),∴cos$α=\sqrt{1-(\frac{2}{3})^{2}}=\frac{\sqrt{5}}{3}$.
(1)sin2α=2sinαcosα=2×$\frac{2}{3}×\frac{\sqrt{5}}{3}$=$\frac{4\sqrt{5}}{9}$,
cos2α=$1-2si{n}^{2}α=1-2×(\frac{2}{3})^{2}=\frac{1}{9}$,
tan2α=$\frac{sin2α}{cos2α}=\frac{\frac{4\sqrt{5}}{9}}{\frac{1}{9}}=4\sqrt{5}$;
(2)sin(α+$\frac{π}{6}$)=sinαcos$\frac{π}{6}$+cosαsin$\frac{π}{6}$=$\frac{2}{3}×\frac{\sqrt{3}}{2}+\frac{\sqrt{5}}{3}×\frac{1}{2}=\frac{2\sqrt{3}+\sqrt{5}}{6}$,
cos(α+$\frac{π}{3}$)=cosαcos$\frac{π}{3}$-sinαsin$\frac{π}{3}$=$\frac{\sqrt{5}}{3}×\frac{1}{2}-\frac{2}{3}×\frac{\sqrt{3}}{2}=\frac{\sqrt{5}-2\sqrt{3}}{6}$,
tan(α+$\frac{π}{4}$)=$\frac{tanα+tan\frac{π}{4}}{1-tanαtan\frac{π}{4}}$=$\frac{\frac{2\sqrt{5}}{5}+1}{1-\frac{2\sqrt{5}}{5}}=\frac{9+4\sqrt{5}}{3}$.
点评 本题考查三角函数的化简求值,考查了同角三角函数基本关系式的应用,考查了两角和的正弦、余弦和正切公式的应用,是中档题.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:解答题
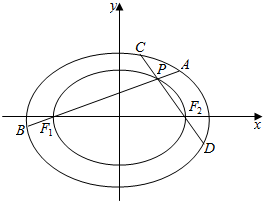 如图,已知点F1,F2是椭圆C1:$\frac{{x}^{2}}{2}$+y2=1的两个焦点,椭圆C2:$\frac{{x}^{2}}{2}$+y2=λ经过点F1,F2,点P是椭圆C2上异于F1,F2的任意一点,直线PF1和PF2与椭圆C1的交点分别是A,B和C,D,设AB、CD的斜率为k,k′.
如图,已知点F1,F2是椭圆C1:$\frac{{x}^{2}}{2}$+y2=1的两个焦点,椭圆C2:$\frac{{x}^{2}}{2}$+y2=λ经过点F1,F2,点P是椭圆C2上异于F1,F2的任意一点,直线PF1和PF2与椭圆C1的交点分别是A,B和C,D,设AB、CD的斜率为k,k′.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com