
分析 化简M=$\frac{1+2\frac{b}{a}+(\frac{b}{a})^{2}}{\frac{b}{a}-1}$,从而令$\frac{b}{a}$=t,t>1;从而化简M=$\frac{{t}^{2}+2t+1}{t-1}$=(t-1)+$\frac{4}{t-1}$+4,利用基本不等式求最小值.
解答 解:M=$\frac{{a}^{2}+2ab+{b}^{2}}{ab-{a}^{2}}$=$\frac{1+2\frac{b}{a}+(\frac{b}{a})^{2}}{\frac{b}{a}-1}$,
令$\frac{b}{a}$=t,由b>a>0知t>1;
故M=$\frac{{t}^{2}+2t+1}{t-1}$=(t-1)+$\frac{4}{t-1}$+4≥8,
(当且仅当t-1=$\frac{4}{t-1}$,即t=3时,等号成立);
故答案为:8.
点评 本题考查了学生的化简能力及基本不等式的应用.


科目:高中数学 来源: 题型:选择题
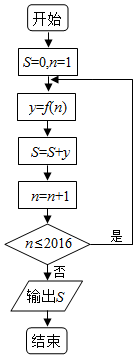
| A. | 0 | B. | 671.5 | C. | 671 | D. | 672 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)的最小正周期为π | B. | x=$\frac{π}{2}$是f(x)的一条对称轴 | ||
| C. | f(x)在(-$\frac{π}{4}$,$\frac{π}{4}$)上单调递增 | D. | |f(x)|的值域是[0,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a=0,b=-1 | B. | a=2,b=1 | C. | a=-π,b=π | D. | a=0,b=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-1<x<2} | B. | {x|x≤-1或x$≥\frac{3}{2}$} | C. | {x|0<x<$\frac{3}{2}$} | D. | {x|x≤0或x≥2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com