
三棱锥P-ABC中,PC、AC、BC两两垂直,BC=PC=1,AC=2,E、F、G分别是AB、AC、AP的中点。
(1)证明:平面GFE//平面PCB;
(2)求二面角B-AP-C的正切值;
(3)求直线PF与平面PAB所成角的正弦值。
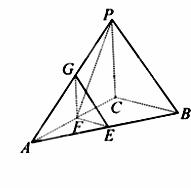
解答:(1)因为E、F、G分别是AB、AC、AP的中点,所以EF//BC,GF//CP。因为EF,GF 平面PCB,所以EF//平面PCB,GF//平面PCB。又EF∩GF=F,所以平面GFE//平面PCB。
平面PCB,所以EF//平面PCB,GF//平面PCB。又EF∩GF=F,所以平面GFE//平面PCB。
(2)过点C在平面PAC内作CH⊥PA,垂足为H,连接HB。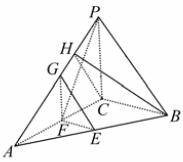 因为BC⊥PC,BC⊥AC,且PC∩AC=C,所以BC⊥平面PAC,所以HB⊥PA,所以∠BHC是二面角B-AP-C的平面角。依条件容易求出CH=
因为BC⊥PC,BC⊥AC,且PC∩AC=C,所以BC⊥平面PAC,所以HB⊥PA,所以∠BHC是二面角B-AP-C的平面角。依条件容易求出CH=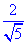 ,所以tan∠BHC=
,所以tan∠BHC=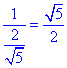 ,所以二面角B-AP-C的正切值是
,所以二面角B-AP-C的正切值是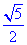 。
。
(3)如图,设PB的中点为K,连接KC,AK,因为ΔPCB为等腰直角三角形,所以KC⊥PB;又AC⊥PC,AC⊥BC,且PC∩BC=C,所以AC⊥平面PCB,所以AK⊥PB,又因为AK∩KC=K,所以PB⊥平面AKC;又PB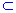 平面PAB,所以平面AKC⊥平面PAB。在平面AKC内,过点F作FM⊥AK,垂足为M。因为平面AKC⊥平面PAB,所以FM⊥平面PAB,连接PM,则∠MPF是直线PF与平面PAB所成的角。容易求出PF=
平面PAB,所以平面AKC⊥平面PAB。在平面AKC内,过点F作FM⊥AK,垂足为M。因为平面AKC⊥平面PAB,所以FM⊥平面PAB,连接PM,则∠MPF是直线PF与平面PAB所成的角。容易求出PF=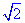 ,FM=
,FM=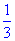 ,所以sin∠MPF=
,所以sin∠MPF=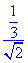 =
=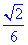 .即直线PF与平面PAB所成的角的正弦值是
.即直线PF与平面PAB所成的角的正弦值是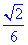


 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源: 题型:
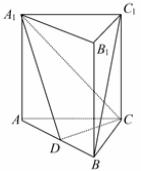
如图,在直三棱柱ABC-A1B1C1中,AC=BC,点D是AB的中点。
(1)求证:BC1//平面CA1D;
(2)求证:平面CA1D⊥平面AA1B1B。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com