
分析 (Ⅰ)原不等式转化为:$\left\{\begin{array}{l}x≥1\\ x-1+x+1≤4\end{array}\right.$或$\left\{\begin{array}{l}-1≤x<1\\-x+1+x+1≤4\end{array}\right.$或$\left\{\begin{array}{l}x<-1\\-x+1-x-1≤4\end{array}\right.$.的并集:求解即可.
(Ⅱ)转化不等式|x+3|+|x+a|<x+6为|x+a|<3,利用子集关系列出不等式组,即可求解实数a的取值范围.
解答 解:(Ⅰ)不等式f(x)≤4的是解集以下3个不等式组解集的并集:$\left\{\begin{array}{l}x≥1\\ x-1+x+1≤4\end{array}\right.$或$\left\{\begin{array}{l}-1≤x<1\\-x+1+x+1≤4\end{array}\right.$或$\left\{\begin{array}{l}x<-1\\-x+1-x-1≤4\end{array}\right.$.
解得不等式f(x)≥4解集为{x|-2≤x≤2}.…(5分)
(Ⅱ)在-2≤x≤2时,不等式|x+3|+|x+a|<x+6等价于|x+a|<3,等价于-a-3<x<-a+3.从而[-2,2]⊆(-a-3,-a+3),所以$\left\{\begin{array}{l}-a-3<-2\\-a+3>2\end{array}\right.$,得实数a的取值范围是{a|-1<a<1}.…(10分)
点评 本题考查绝对值表达式的解法,考查分析问题解决问题的能力.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:解答题
 如图所示,已知双曲线的中心在坐标原点O,焦点分别是F1(-2,0),F2(2,0),且双曲线上的任意一点到两个焦点的距离之差的绝对值等于2.
如图所示,已知双曲线的中心在坐标原点O,焦点分别是F1(-2,0),F2(2,0),且双曲线上的任意一点到两个焦点的距离之差的绝对值等于2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\sqrt{3}$ | B. | -$\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
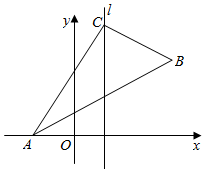 如图,△ABC的顶点坐标分别为A(-3,0),B(9,5),C(3,9),直线l过点C且把三角形的面积分为1:1的两部分,则l的方程是5x-12y+93=0.
如图,△ABC的顶点坐标分别为A(-3,0),B(9,5),C(3,9),直线l过点C且把三角形的面积分为1:1的两部分,则l的方程是5x-12y+93=0.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com