
分析 (1)求出f(x)的定义域确定出A,求出g(x)的定义域确定出B即可;
(2)由A与B,求出两集合的并集,找出A补集与B补集的交集即可.
解答 解:(1)由f(x)=lg$\frac{1+x}{1-x}$,得到$\frac{1+x}{1-x}$>0,即(x+1)(x-1)<0,
解得:-1<x<1,即A=(-1,1),
函数g(x)=$\sqrt{3-x}$,得到3-x≥0,即x≤3,
∴B=(-∞,3];
(2)∵A=(-1,1),B=(-∞,3],
∴A∪B=(-∞,3],∁RA=(-∞,-1]∪[1,+∞),∁RB=(3,+∞),
则(∁RA)∩(∁RB)=(3,+∞).
点评 此题考查了交、并、补集的混合运算,以及函数定义域及其求法,熟练掌握各自的定义是解本题的关键.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{5}$ | B. | $\frac{2}{5}$或-2 | C. | $\frac{3}{5}$ | D. | $\frac{3}{5}$或-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6-4$\sqrt{2}$ | B. | 3-2$\sqrt{2}$ | C. | 2$\sqrt{2}$-3 | D. | 4$\sqrt{2}$-6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{π}{3}$ | B. | -$\frac{5π}{6}$ | C. | -$\frac{2π}{3}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
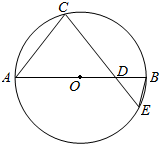 如图,AB是圆O的直径,弦CE交AB于D,CD=4$\sqrt{2}$,DE=2$\sqrt{2}$,BD=2.
如图,AB是圆O的直径,弦CE交AB于D,CD=4$\sqrt{2}$,DE=2$\sqrt{2}$,BD=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com