
分析 (Ⅰ)直线l的极坐标方程展开得:$ρsinθ+ρcosθ-\sqrt{2}m$=0,由此能求出直线l的直角坐标方程.
(Ⅱ)曲线C的普通方程为:(x-1)2+(y-1)2=2,曲线C是一个圆,圆心C到直线l的距离$d=\frac{|1+1-\sqrt{2}m|}{\sqrt{2}}$$≤\frac{3\sqrt{2}}{2}$,由此能求出结果.
解答 解:(Ⅰ)直线l的极坐标方程为:ρsin(θ+$\frac{π}{4}$)=m(m∈R).
展开得:$ρsinθ+ρcosθ-\sqrt{2}m$=0,…(3分)
所以直线l的直角坐标方程为:x+y-$\sqrt{2}m$=0.…(5分)
(Ⅱ)曲线C的普通方程为:(x-1)2+(y-1)2=2,
所以曲线C是一个圆;…(7分)
由已知可得,圆心C到直线l的距离$d=\frac{|1+1-\sqrt{2}m|}{\sqrt{2}}$$≤\frac{3\sqrt{2}}{2}$,…(9分)
解得-$\frac{\sqrt{2}}{2}≤m≤\frac{5\sqrt{2}}{2}$.…(10分)
点评 本题考查直线的直角坐标方程的求法,考查实数的取值范围的求法,是中档题,解题时要认真审题,注意极坐标方程、直角坐标方程互化公式的合理运用.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{1}{3}$,+∞) | B. | (-$\frac{1}{3}$,1) | C. | (-$\frac{1}{3}$,$\frac{1}{3}$) | D. | (-∞,-$\frac{1}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=2x-2-x | B. | y=cosx | C. | y=log2|x| | D. | y=x+x-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
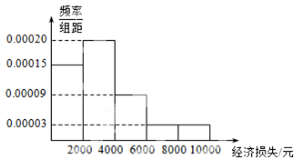 适逢暑假,小王在某小区调查了50户居民由于洪灾造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出频率分布直方图(如图).
适逢暑假,小王在某小区调查了50户居民由于洪灾造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出频率分布直方图(如图).| 经济损失不超过4000元 | 经济损失超过4000元 | 合计 | |
| 捐款超过500元 | 30 | 9 | 39 |
| 捐款不超过500元 | 5 | 6 | 11 |
| 合计 | 35 | 15 | 50 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图所示的三角形数阵角“莱布尼兹调和三角形”,它是由整数的倒数组成的,第n行有n个数,且两端的数均为$\frac{1}{n}({n≥2})$,每个数使它下一行左右相邻两个数的和,如$\frac{1}{1}=\frac{1}{2}+\frac{1}{2},\frac{1}{2}=\frac{1}{3}+\frac{1}{6},\frac{1}{3}=\frac{1}{4}+\frac{1}{12}$,则第7行第5个数(从左到右)为$\frac{1}{105}$.
如图所示的三角形数阵角“莱布尼兹调和三角形”,它是由整数的倒数组成的,第n行有n个数,且两端的数均为$\frac{1}{n}({n≥2})$,每个数使它下一行左右相邻两个数的和,如$\frac{1}{1}=\frac{1}{2}+\frac{1}{2},\frac{1}{2}=\frac{1}{3}+\frac{1}{6},\frac{1}{3}=\frac{1}{4}+\frac{1}{12}$,则第7行第5个数(从左到右)为$\frac{1}{105}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{5π}{3}$ | B. | $\frac{10π}{3}$ | C. | $\frac{11π}{3}$ | D. | $\frac{22π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
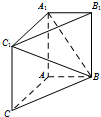 如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.
如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com