
 如图所示的三角形数阵角“莱布尼兹调和三角形”,它是由整数的倒数组成的,第n行有n个数,且两端的数均为$\frac{1}{n}({n≥2})$,每个数使它下一行左右相邻两个数的和,如$\frac{1}{1}=\frac{1}{2}+\frac{1}{2},\frac{1}{2}=\frac{1}{3}+\frac{1}{6},\frac{1}{3}=\frac{1}{4}+\frac{1}{12}$,则第7行第5个数(从左到右)为$\frac{1}{105}$.
如图所示的三角形数阵角“莱布尼兹调和三角形”,它是由整数的倒数组成的,第n行有n个数,且两端的数均为$\frac{1}{n}({n≥2})$,每个数使它下一行左右相邻两个数的和,如$\frac{1}{1}=\frac{1}{2}+\frac{1}{2},\frac{1}{2}=\frac{1}{3}+\frac{1}{6},\frac{1}{3}=\frac{1}{4}+\frac{1}{12}$,则第7行第5个数(从左到右)为$\frac{1}{105}$. 分析 根据题意,设“莱布尼兹调和三角形”中第n行第m个数为a(n,m),归纳可得每一行的第一个数字就是这个行数的倒数,且两个数字之和等于两个数字上方的数字之和,可得a(5,1)、a(6,1)、a(7,1)的值,进而可得a(7,2)与a(6,2)的值,而又由a(7,3)=a(6,2)-a(7,2),计算可得a(7,3)的值,结合“莱布尼兹调和三角形”的对程性,分析可得答案.
解答 解:根据题意,设“莱布尼兹调和三角形”中第n行第m个数为a(n,m),
由于“莱布尼兹调和三角形”中,每一行的第一个数字就是这个行数的倒数,且两个数字之和等于两个数字上方的数字之和,
则a(5,1)=$\frac{1}{5}$,a(6,1)=$\frac{1}{6}$,a(7,1)=$\frac{1}{7}$,
a(7,2)=a(6,1)-a(7,1)=$\frac{1}{42}$,a(6,2)=a(5,1)-a(6,1)=$\frac{1}{30}$,
a(7,3)=a(6,2)-a(7,2)=$\frac{1}{30}$-$\frac{1}{42}$=$\frac{1}{105}$,
根据“莱布尼兹调和三角形”的对程性,分析可得a(7,5)=a(7,3)=$\frac{1}{105}$;
故答案为:$\frac{1}{105}$.
点评 本题考查归纳推理,是一个数列问题,解题的关键是归纳出每一行的第一个数字就是这个行数的倒数,且两个数字之和等于两个数字上方的数字之和.


科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
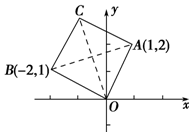 如图在复平面上,一个正方形的三个顶点对应的复数分别是1+2i,-2+i,0,那么这个正方形的第四个顶点对应的复数为( )
如图在复平面上,一个正方形的三个顶点对应的复数分别是1+2i,-2+i,0,那么这个正方形的第四个顶点对应的复数为( )| A. | 3+i | B. | -1+3i | C. | 1-3i | D. | 3-i |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
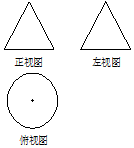 如图,一个空间几何体正视图与左视图为全等的等边三角形,俯视图为一个半径为1的圆及其圆心,那么这个几何体的表面积为( )
如图,一个空间几何体正视图与左视图为全等的等边三角形,俯视图为一个半径为1的圆及其圆心,那么这个几何体的表面积为( )| A. | π | B. | 3π | C. | 2π | D. | $π+\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com