
分析 移项得$\sqrt{{x}^{2}-λ}$=x-2$\sqrt{{x}^{2}-1}$,求出右侧函数的单调性和值域,根据方程有解可判断出解的范围,利用函数图象得出不等式从而得出λ的范围.
解答 解:∵$\sqrt{{x^2}-λ}+2\sqrt{{x^2}-1}=x$,
∴$\sqrt{{x}^{2}-λ}$=x-2$\sqrt{{x}^{2}-1}$,
令f(x)=x-2$\sqrt{{x}^{2}-1}$(x≥1或x≤-1),
显然当x≤-1时,f(x)<0,
∴方程$\sqrt{{x}^{2}-λ}$=x-2$\sqrt{{x}^{2}-1}$无解,
当x≥1时,f′(x)=1-$\frac{2x}{\sqrt{{x}^{2}-1}}$=$\frac{\sqrt{{x}^{2}-1}-2x}{\sqrt{{x}^{2}-1}}$,
∵x2-1-4x2=-3x2-1<0,
∴x2-1<4x2,即$\sqrt{{x}^{2}-1}$<2x,∴f′(x)<0,
∴f(x)在[1,+∞)上单调递减,
令f(x)=0得x=2$\sqrt{{x}^{2}-1}$,解得x=$\frac{2}{\sqrt{3}}$,
∴当1≤x≤$\frac{2}{\sqrt{3}}$时,f(x)≥0,当x$>\frac{2}{\sqrt{3}}$时,f(x)<0,
∴方程$\sqrt{{x}^{2}-λ}$=x-2$\sqrt{{x}^{2}-1}$的解必在区间[1,$\frac{2}{\sqrt{3}}$]上.
令g(x)=$\sqrt{{x}^{2}-λ}$(1≤x≤$\frac{2}{\sqrt{3}}$),
(1)当λ=0时,g(x)=x,∴g(1)=1,又f(1)=1,
∴x=1为方程$\sqrt{{x}^{2}-λ}$=x-2$\sqrt{{x}^{2}-1}$的解,符合题意;
(2)当λ<0时,g(x)=$\sqrt{{x}^{2}-λ}$>g(1)=$\sqrt{1-λ}$>1,
而f(x)≤f(1)=1,
∴方程$\sqrt{{x}^{2}-λ}$=x-2$\sqrt{{x}^{2}-1}$无解,不符合题意;
(3)当λ>0,令y=g(x)=$\sqrt{{x}^{2}-λ}$,
则$\frac{{x}^{2}}{λ}-\frac{{y}^{2}}{λ}=1$,∴g(x)的图象为等轴双曲线右支在第一象限内的部分(含右顶点),
双曲线的右顶点为($\sqrt{λ}$,0),
做出f(x)和g(x)的函数图象如图所示: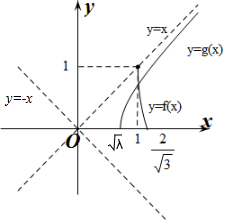
∵方程g(x)=f(x)在[1,$\frac{2}{\sqrt{3}}$]上有解,∴0<$\sqrt{λ}$$≤\frac{2}{\sqrt{3}}$,
即0<λ≤$\frac{4}{3}$.
综上,0≤λ≤$\frac{4}{3}$.
故答案为:$[{0,\frac{4}{3}}]$.
点评 本题考查了函数的单调性判断,函数零点与函数图象的关系,分类讨论思想,属于中档题.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
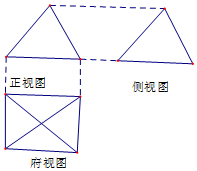 如图,一个简单空间几何体的三视图与侧视图都是边长为2的正三角形,俯视图是正方形,则此几何体的侧面积是( )
如图,一个简单空间几何体的三视图与侧视图都是边长为2的正三角形,俯视图是正方形,则此几何体的侧面积是( )| A. | $4+4\sqrt{3}$ | B. | 8 | C. | $4\sqrt{3}$ | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
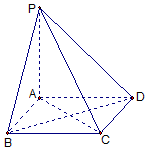 如图,棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=AB=2.
如图,棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=AB=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-2} | B. | {-1,0} | C. | {-1,0,1} | D. | {-2,-1,0,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2) | B. | (-∞,-2] | C. | (-∞,4) | D. | (4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com