
分析 问题转化为a>$\frac{{e}^{x}+x}{{e}^{-x}-x-2}$,设h(x)=$\frac{{e}^{x}+x}{{e}^{-x}-x-2}$利用极限的思想求出函数h(x)的最大值,问题得以解决.
解答 解:∵f(x)=ex-ae-x+(a+1)x+2a,对于任意的x∈(0,+∞),都有f(x)>0,
∴ex+x>a(e-x-x-2),
∵g(x)=e-x-x-2在(0,+∞)为减函数,
∴g(x)max<g(0)=-1,
∴g(x)<-1,
∴a>$\frac{{e}^{x}+x}{{e}^{-x}-x-2}$,
设h(x)=$\frac{{e}^{x}+x}{{e}^{-x}-x-2}$,
∴$\underset{lim}{x→0}$=$\frac{{e}^{x}+x}{{e}^{-x}-x-2}$
=$\underset{lim}{x→0}$=$\frac{{e}^{x}}{-{e}^{-x}}$=-1,
∴a≥-1,
故a的取值范围为[-1,+∞).
点评 本题考查了参数的取值范围以及函数恒成立的问题和极限的思想,属于中档题.


 寒假学与练系列答案
寒假学与练系列答案科目:高中数学 来源: 题型:填空题
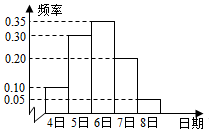 北京铁路局针对今年春运客流量进行数据整理,调查北京西站从2月4日到2月8日的客流量,根据所得数据画出了五天中每日客流量的频率分布图,为了更详细地分析不同时间的客流人群,按日期用分层抽样的方法抽样,若从2月7日这个日期抽取了40人,则一共抽取的人数为200.
北京铁路局针对今年春运客流量进行数据整理,调查北京西站从2月4日到2月8日的客流量,根据所得数据画出了五天中每日客流量的频率分布图,为了更详细地分析不同时间的客流人群,按日期用分层抽样的方法抽样,若从2月7日这个日期抽取了40人,则一共抽取的人数为200.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
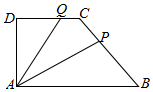 如图,在直角梯形ABCD中,AB∥CD,AB=2,AD=DC=1,P是线段BC上一动点,Q是线段DC上一动点,$\overrightarrow{DQ}=λ\overrightarrow{DC}$,$\overrightarrow{CP}=(1-λ)\overrightarrow{CB}$,若集合M=$\{x|x=\overrightarrow{AP}•\overrightarrow{AQ}\}$,N=$\left\{{x\left|{x=\frac{{{a^2}+{b^2}+1}}{3(a-b)},a>b,ab=1}\right.}\right\}$.则M∩N=[$\frac{2\sqrt{3}}{3}$,2].
如图,在直角梯形ABCD中,AB∥CD,AB=2,AD=DC=1,P是线段BC上一动点,Q是线段DC上一动点,$\overrightarrow{DQ}=λ\overrightarrow{DC}$,$\overrightarrow{CP}=(1-λ)\overrightarrow{CB}$,若集合M=$\{x|x=\overrightarrow{AP}•\overrightarrow{AQ}\}$,N=$\left\{{x\left|{x=\frac{{{a^2}+{b^2}+1}}{3(a-b)},a>b,ab=1}\right.}\right\}$.则M∩N=[$\frac{2\sqrt{3}}{3}$,2].查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com