
分析 利用正弦定理把已知等式化边为角,求出B,可得三角形为等边三角形,则面积可求.
解答 解:△ABC中,∵b=2acosB,
∴根据正弦定理,得sinB=2sinAcosB,
又∵A=$\frac{π}{3}$,
∴sinB=2sin$\frac{π}{3}$cosB,
即sinB=$\sqrt{3}$cosB,可得tanB=$\sqrt{3}$.
∵B∈(0,π),∴B=$\frac{π}{3}$;
∵A=$\frac{π}{3}$,B=$\frac{π}{3}$,
∴C=π-(A+B)=$\frac{π}{3}$.
则a=b=c=1,
∴S△ABC=$\frac{1}{2}×1×1×sin\frac{π}{3}=\frac{\sqrt{3}}{4}$.
故答案为:$\frac{\sqrt{3}}{4}$.
点评 本题已知三角形的边和角的关系式,求三角形的面积,着重考查了正弦定理、同角三角函数的基本关系与三角形的面积求法等知识,属于中档题.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
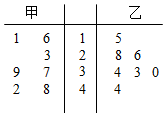 甲、乙两名篮球运动员在7场比赛中的得分情况如茎叶所示,$\overline x$甲、$\overline x$乙分别表示甲、乙两人的平均得分,则下列判断正确的是( )
甲、乙两名篮球运动员在7场比赛中的得分情况如茎叶所示,$\overline x$甲、$\overline x$乙分别表示甲、乙两人的平均得分,则下列判断正确的是( )| A. | $\overline x$甲>$\overline x$乙,甲比乙得分稳定 | B. | $\overline x$甲>$\overline x$乙,乙比甲得分稳定 | ||
| C. | $\overline x$甲<$\overline x$乙,甲比乙得分稳定 | D. | $\overline x$甲<$\overline x$乙,乙比甲得分稳定 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{3}$ | D. | -$\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com