
分析 先求出第一个不等式得到x的取值范围,利用积分的几何意义进行求解即可.
解答 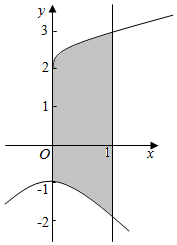 解:由$\sqrt{1-x}$≤1得0≤1-x≤1,即0≤x≤1,
解:由$\sqrt{1-x}$≤1得0≤1-x≤1,即0≤x≤1,
则由积分的性质可知平面区域Ω的面积S=∫${\;}_{0}^{1}$[2+$\sqrt{x}$-(-1-x2)dx═∫${\;}_{0}^{1}$(3+$\sqrt{x}$+x2)dx=($\frac{1}{3}$x3+3x+$\frac{2}{3}$x${\;}^{\frac{3}{2}}$)|${\;}_{0}^{1}$=$\frac{1}{3}$+3+$\frac{2}{3}$=4,
故答案为:4.
点评 本题主要考查区域的面积的计算,利用积分的几何意义是解决本题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=sinx | B. | f(x)=2cosx+1 | C. | f(x)=2x-1 | D. | $f(x)=ln\frac{1-x}{1+x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\frac{{\sqrt{5}}}{3}$ | C. | $\frac{{\sqrt{13}}}{2}$ | D. | $\frac{{\sqrt{13}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
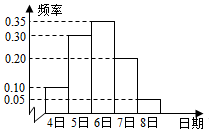 北京铁路局针对今年春运客流量进行数据整理,调查北京西站从2月4日到2月8日的客流量,根据所得数据画出了五天中每日客流量的频率分布图,为了更详细地分析不同时间的客流人群,按日期用分层抽样的方法抽样,若从2月7日这个日期抽取了40人,则一共抽取的人数为200.
北京铁路局针对今年春运客流量进行数据整理,调查北京西站从2月4日到2月8日的客流量,根据所得数据画出了五天中每日客流量的频率分布图,为了更详细地分析不同时间的客流人群,按日期用分层抽样的方法抽样,若从2月7日这个日期抽取了40人,则一共抽取的人数为200.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com